# 编译原理 <!-- >徐达丽 13804582160 36302997 >10%平时+10%实验+阶段（至语法分析）（6:4）40%+期末（4:6）40% --> ## 1 绪论 ### 1.1 编译的概念 $\require{extpfeil}\Newextarrow{\xRightarrow}{5,5}{0x21D2}$高级语言（类似于数学定义或自然语言的简洁形式）$\xrightarrow[Compiling]{编译}$汇编语言（引入了助记符，但依然不便于编写）$\xrightarrow[Assenbling]{汇编}$机器语言（可以直接被计算机直接理解的二进制语言） 编译程序：将高级语言程序翻译成汇编语言或机器语言程序的翻译程序 解释程序：一边解释一边执行的翻译程序 ### 1.2 编译的过程 编译的过程通常可以理解成如下五个阶段，但需要注意的是，这种划分**并非是刻板绝对**的，这样分析只是为了便于理解 词法分析(Lexical Analysis)$\rightarrow$语法分析(Parsing)$\rightarrow$语义分析与中间代码生成(Semantic Analysis)$\rightarrow$代码优化(Optimization)$\rightarrow$目标代码生成(Code generation) 我们通过如下的源程序来便于理解编译的过程 ```cpp= float r,h,s; s=2*3.14*r*(h+r); ``` #### 词法分析 * 识别出源程序中的一个个单词符号 * 功能：从左向右逐行扫描源程序的字符，识别出各个单词，确定**单词的种别** * 将识别出的单词转换成统一的机内表示——词法单元（token）的形式 * token：<种别码，属性值> * *种别码对应一个单词的种别，没有规范要求，提前约定好即可* * 例如 ``` <关键词，float> <标识符，r> <分界符，;> <算符，=> <常数，3.14> ``` #### 语法分析 * 功能：从词法分析器输出的token序列中识别出各类短语，并构造**语法分析树** * 语法分析树描述了句子的语法结构 * [附图] #### 语义分析与中间代码生成 * 功能：分析由语法分析器给出的语法单位的语义 * 获取标识符的属性 *标识符在整个编译过程中将会通过符号表加以记录* * 类型 * 存储位置及长度 * 值 * 作用域 * 语义检查 * 变量或函数未经声明就使用 * 变量或过程名重复声明 * 运算分量类型不匹配 * 操作符与操作数之间的类型不匹配 * 中间代码 *一种意义明确，便于处理的记号系统，通常独立于具体的硬件系统。与机器指令较接近，易于转换成机器指令* * 波兰表示 * **逆波兰式** $(a+b)*(a-b)\rightarrow ab+ab-*$ * 三元式 * 四元式 三元四元式在某种程度上对应二叉语法分析树 会产生大量的中间变量，因此需要经过代码优化 ```cpp= t1=2*3.14; t2=t1*r; t3=h+r; t4=t2*t3; s=t4; ``` * 语法分析树 #### 代码优化 * 功能：对代码进行**等价变换**以求提高效率——提高运行速度和节省存储空间 * 与机器无关的优化 * 局部优化 * 合并常量 * 基本块内公共子表达式的提取 * 全局优化 * 循环优化 * 削弱运算强度 * 与机器有关的优化 * 高效利用寄存器等硬件 * 根据体系结构进行并行化处理 * 高效利用多级存储体系 ```cpp= t2=6.28*r; t3=h+r; s=t2*t3 ``` #### 目标代码生成 * 功能：将中间代码变换成特定机器上的低级语言代码 ```asm= mov AX,6.28 mul r mov t2,AX mov AX,h mov AX,r mov t3,AX mov AX,t2 mul t3 mov s,AX ``` #### 编译程序结构框图  #### 表格与表格管理 功能：管理各种符号表（常数、标号、变量、过程、结构...） * 查，填源程序中出现的符号和编译程序生成的符号，为编译的各个阶段提供信息 * 辅助语法分析，语义分析 | 名称 | 种类 | 类型 | 层次 | 偏移量 | | ---- | ---- | ----- | ---- | ------ | | r | 变量 | float | 1 | d | | h | 变量 | float | 1 | d+4 | | s | 变量 | float | 1 | d+8 | ### 1.3 编译的遍（Pass） 遍（Pass）：对输入文件（源程序或其等价的中间形式）从头到尾扫描一遍，并完成预定处理工作的过程 在每一遍扫描中均可以完成不同的任务，与理论过程并不完全一致 ### 1.4 编译程序的生成 1. T型图  2. 自展  3. 移植  ## 2 程序设计语言及文法 ### 2.2 基本概念 * 字母表(Alphabet) * 字母表$\Sigma$是一个有穷非空符号集合 * 符号：字母、数字、标点符号... * 特点：整体性，可辨认性 * 字母表上的运算 * 字母表$\Sigma_1$和$\Sigma_2$的乘积为$\Sigma_1\Sigma_2=\{ab|a\in \Sigma_1,b\in \Sigma_2\}$ * 字母表$\Sigma$的$n$次幂（递归定义）： $\begin{align} \left\{\begin{matrix} \Sigma^0 =\{\varepsilon\} \\ \Sigma^n=\Sigma^{n-1}\Sigma,\ \ n\geq1 \end{matrix}\right. \end{align}$ 字母表的n次幂：长度为n的符号串构成的集合 * 字母表$\Sigma$的正闭包$\Sigma^+$： $\sum^+=\sum\cup\sum^2\cup\sum^3...$ 字母表的正闭包：长度为正数的符号串构成的集合 * 字母表$\Sigma$的克林闭包$\Sigma^*$： 在字母表$\Sigma$的正闭包的基础上增加了长度为0的$\varepsilon$ * 串 * 串是字母表符号的一个有穷序列 * 空串是长度为0的串，用$\varepsilon$表示，$|\varepsilon|=0$ * 串的连接： 如果如果$x$和$y$是串，那么$x$和$y$的连接是把$y$附加到$x$后面而形成的串，记作$xy$ 对于任何字符串$s$都有$\varepsilon s=s \varepsilon =s$ 单位元是集合里的一种特别的元，当它和其他元素结合时，并不会改变那些元素。也叫**幺元**（么元）。若$a\times e=a$，$e$称为右单位元；若$e\times a=a$，$e$称为左单位元，若$a\times e=e\times a=a$，则$e$称为单位元 * 串的幂： 串$s$的$n$次幂：将$n$个$s$顺次连接起来 ### 2.3 文法的定义 #### 2.3.1 语言的形式化内容提取 语言(Language)：组成程序的**所有语句的集合** 程序(Program)：满足语法规则的**语句序列** 语句(Sentence)：满足语法规则的**单词序列** 单词(Token) ：满足词法规则的**字符串** 字符(Character) ：组成字符串的**最小单位** 分析语言的过程就是**自底而上**的过程 举例来说，我们可以认为一个赋值语句具有下列形式： 1. **左部量$=$右部表达式** 2. 左部量可以是简单变量、下标变量等。一般来说，简单变量可以简单理解为$vara,varb,varc$，而下标变量则可以认为是$var[1],var[2],var[3]$ 3. 右部表达式则可以是由$+，-$运算符所连接组成的两个简单变量或下标变量 $\downarrow$ 此时我们就可以将上述**自然语言的约定**转化成一个较为规范的形式表达 $\downarrow$ 1. “赋值语句”是“左部量$\rightarrow$右部表达式” 2. “左部量”是“简单变量”或者“下标变量” 3. “简单变量”是$vara,varb$或者$varc$ 4. “下标变量”是$var[1],var[2],var[3]$ 5. “右部表达式”是“简单变量”或者“下标变量”连接上“运算符”，再连接上“简单变量”或者“下标变量” 6. “运算符”是$+$或$-$ $\downarrow$ 进一步的，我们可以将其转化为一个更加准确的定义表达 $\downarrow$ 1. <赋值语句>定义为<左部量>=<右部表达式> 2. <左部量>定义为<简单变量>或者<下标变量> 3. <简单变量>定义为$vara,varb$或者$varc$ 4. <下标变量>定义为$var[1],var[2],var[3]$ 5. <右部表达式>定义为<简单变量>或者<下标变量>连接上<运算符>，再连接上<简单变量>或者<下标变量> 6. <运算符>定义为$+$或$-$ $\downarrow$ 最终我们就可以完成最初的对自然语言定义的形式化提取 $\downarrow$ 1. <赋值语句>$\rightarrow$<左部量>$=$<右部表达式> 2. <左部量>$\rightarrow$<简单变量> 3. <左部量>$\rightarrow$<下标变量> 4. <简单变量>$\rightarrow vara$ 5. <简单变量>$\rightarrow varb$ 6. <简单变量>$\rightarrow varc$ 7. <下标变量>$\rightarrow m[1]$ 8. <下标变量>$\rightarrow m[2]$ 9. <下标变量>$\rightarrow m[3]$ 10. <右部表达式>$\rightarrow$<简单变量><运算符><简单变量> 11. <右部表达式>$\rightarrow$<下标变量><运算符><简单变量> 12. <右部表达式>$\rightarrow$<简单变量><运算符><下标变量> 13. <右部表达式>$\rightarrow$<下标变量><运算符><下标变量> 14. <运算符>$\rightarrow +$ 15. <运算符>$\rightarrow -$ 通过对以上过程的分析和理解，我们得到以下四个表示语言所需要的要素 1. 形如"<运算符>"等的一系列符号，他们表示相应语言结构中某个位置上可能出现的内容，每个符号对应的是一个集合，这种符号代表一个"语法范畴"，是一种语法变量，不实际出现在语句中，称之为**非终结符** 2. 特殊的语法成分如"<赋值语句>"，这里所有的规则都是为了说明"<赋值语句>"而存在的，因此称之为**开始符号** 3. $vara,varb,varc$等出现在语句中，他们仅表示自身，称之为**终结符** 4. 各种形式化规则$\alpha \rightarrow \beta$，称之为**产生式** #### 2.3.2 文法的形式化定义 我们用$G=(V_T,V_N,P,S)$四元组去形式化的定义文法 * $V_T$：终结符集合 * 终结符是文法所定义语言的基本符号，有时也称之为token * 如上例：$V_T=\{va,vb,vc,var[1],var[2],var[3]\}$ * $V_N$：非终结符集合 * 非终结符是用来表示语法成分的符号，有时也称之为语法变量 * 如上例：$V_N=\{$<赋值语句>,<左部量>...$\}$ * 需要注意：$V_T\cap V_N=\emptyset$，$V_T\cup V_N=$文法符号集 * $P$：产生式集合 * 产生式描述了将终结符和非终结符组合成串的方法 * 产生式的一般形式为：$\alpha \rightarrow \beta$ * $\alpha \in (V_T\cup V_N)^+$ * $\beta \in (V_T\cup V_N)^*$ * $S$：开始符号 * 开始符号标识的是该文法中最大的语法成分。$S\in V_N$ * 如上例：$S=$<赋值语句> 在不引起歧义的前提下，可以只写产生式$G$。事实上$G$中已经包含了文法中所有的信息 例如 $G=(\{id,+,(,)\},\{E\},P,E)$，$P=\{E\rightarrow E+E,E\rightarrow (E),E\rightarrow id\}$ 就可以简写为 $G: E\rightarrow E+E,E\rightarrow (E),E\rightarrow id$ #### 2.3.3 产生式的简写 * 对于一组有着相同左部$\alpha$产生式 $\alpha \rightarrow \beta_1,\alpha \rightarrow \beta_2,...,\alpha \rightarrow \beta_n$ 可以简记为$\alpha \rightarrow \beta_1|\beta_2|...|\beta_n$ 其中$\beta_1,\beta_2,...,\beta_n$称为$\alpha$的候选式 如上例中的产生式$G$可以进一步简化为 $E\rightarrow E+E|E*E|(E)|id$ #### 2.3.4 符号约定 * 终结符 * 字母表中排在靠前的小写字母，如$a、b、c$ * 运算符，如$+、*$ * 标点符号，如逗号、括号 * 阿拉伯数字 * 粗体字符串，如$id、if$ * 非终结符 * 字母表中排在靠前的大写字母，如$A、B、C$ * 字母$S$，通常表示文法的开始符号 * 小写、斜体的名字，如$expr、stmt$ * 代表程序构造的大写字母，如$E$（表达式）、$T$（项）、$F$（因子） * 几个约定 * 字母表中排在靠后的大写字母表示文法符号 * 字母表中排在靠后的小写字母表示终结符号串 * 小写希腊字母表示文法符号串 * 除非特别说明，第一个产生式的左部就是开始符号 #### 2.3.5 推导与规约 * 直接推导 给定文法$G=(V_T,V_N,P,S)$，如果$\alpha \rightarrow \beta \in P$，那么就可以讲符号串 $\gamma \alpha \delta$中的$\alpha$替换成$\beta$，也就是说，可以将$\gamma \alpha \delta$重写为$\gamma \beta \delta$，$\gamma \alpha \delta \xRightarrow[G]{} \gamma \alpha \delta$，此时我们称$\gamma \alpha \delta$**直接推导**出$\gamma \beta \delta$ 如果$a\xRightarrow[G]{+}\beta$，则表示$\alpha$可经过**正数步**推导得到$\beta$ 如果$a\xRightarrow[G]{*}\beta$，则表示$\alpha$可经过**若干（可以为0）步**推导得到$\beta$ 简而言之就是用产生式的右边替换产生式的左部 * 规约 规约与推导式一一对应的，二者互为逆过程。句子的推导从生成语言的的角度出发（抽象到具体），句子的规约是从识别语言的角度出发（具体到抽象）  #### 2.3.6 句型和句子 * 如果$S \xRightarrow{*} \alpha$，$\alpha \in (V_T\cup V_N)^*$，则称$\alpha$是文法$G$产生的一个**句型** * 一个句型中既可以包含终结符，也可以包含非终结符，也可以是空串 * 如果$S \xRightarrow{*} w$，$w \in {V_T}^*$，则称$w$是文法$G$的一个句子 * **句子是不包含非终结符的句型**  ### 2.4 语言的定义 #### 2.4.1 语言的形式化定义 * 由文法$G$的开始符号$S$推导出的所有句子构成的集合，称为文法$G$生成的语言，记为$L(G)$ * 即$L(G)=\{w|S \xRightarrow{*} w, w\in {V_T}^*\}$ * 语言形式化定义的根本出发点是为了用有穷文法表示无穷语言，即解决对无穷语言的有穷描述问题 ### 2.5 文法的分类 * 0型文法 * 无限制语法（Unrestricted Grammar）/短语结构文法（Phrase Structure Grammar） * $\forall \alpha \rightarrow \beta \in P$ * 由0型文法$G$产生的语言记作$L(G)$，称作0型语言，也可以称为短语结构语言或可枚举集 * 1型文法 * 上下文有关文法（Content-Sensitive Grammar，CSG) * $\forall \alpha \rightarrow \beta \in P,|\alpha|\leq |\beta|$ * 产生式的一般形式：$\alpha_1 A \alpha_2 \rightarrow \alpha_1 B \alpha_2$ * 2型文法 * 上下文无关文法（Content-Free Grammar，CFG） * 主要应用在语法分析部分 * $\forall \alpha \rightarrow \beta \in P,\alpha \in V_N$ * 产生式的一般形式：$A\rightarrow B$ * 3型文法 * 正则文法（Regular Grammar，RG） * 主要应用在词法分析部分 * 右线性文法：$A\rightarrow wB$或$A\rightarrow w$ * 左线性文法：$A\rightarrow Bw$或$A\rightarrow w$ * $w\in {V_T}^+$ * 就可以得到对语言的描述：$L(G)=\{\alpha |S\xRightarrow{*} \alpha 且\alpha \in V_T^*\}$ * 正则文法例题1： 有正规集是由不以0开始的正奇数组成，给出RG 这个单词事实上可以由三个部分组成 I(非0) II(任意组合) III(1,3,4,5,7,9以满足奇数要求) $\begin{align*} &G=(V_N,V_T,P,S)\\ &V_T=\{0,1,2,3,4,5,6,7,8,9\}\\ &V_N=\{S,A\}\\ &d_1:1-9\\ &d_2:0-9\\ &d_3:1,3,5,7,9\\ P: &1.S\rightarrow d_3\\ &2.S\rightarrow d_1A\\ &3.A\rightarrow d_3\\ &4.A\rightarrow d_2A \end{align*}$ * 正则文法例题2: 给出标识符的正规文法描述 $\begin{align*} &d_1:a-z(eq:L)\\ &d_2:0-9(eq:D)\\ &S\rightarrow d_1\\ &S\rightarrow d_1A\\ &A\rightarrow d_1|d_2\\ &A\rightarrow d_1A|d_2A\\ \end{align*}$ * 正则文法例题3: 给出C语言标识符的正规文法描述 多了额外的标识符 $\begin{align*} &d_1:a-z(L)\\ &d_2:0-9(D)\\ &S\rightarrow d_1|\_\\ &S\rightarrow d_1A|\_A\\ &A\rightarrow d_1|d_2|\_\\ &A\rightarrow d_1A|d_2A|\_A\\ \end{align*}$ * 正则文法例题4: 给出程序设计语言中实常数的正规文法描述 $\begin{align*} &nonZeroDigit: 1|2|3|4|5|6|7|8|9\\ &dgt: 0|1|2|3|4|5|6|7|8|9\\ &octDgt: 0|1|2|3|4|5|6|7\\ &hexDgt: 0|1|2|3|4|5|6|7|8|9|a|b|c|d|e|f\\ &sign: +|-|\varepsilon\\ &<number>\rightarrow \ 0x<hexNum>|\ 0<octNum>|\ <unSigNum>\\ &<hexNum>\rightarrow hexDgt\ <hexNum>|hexDgt \\ &<octNum>\rightarrow octDgt\ <octNum>|octDgt\\ &<unSigNum>\rightarrow nonZeroDigit\ <unSigNumFlo>|0\ <optFrac>|dgt\\ &<unSigNumFlo>\rightarrow dgt\ <unSigNumFlo>|\ dgt\ <optFrac>|dgt\ <optExp>|dgt\\ &<optFrac>\rightarrow .<fracNum> \\ &<fracNum>\rightarrow dgt\ <fracNum>|dgt\ <optExp>\\ &<optExp>\rightarrow e\ sign\ <dgts>\\ &<dgts>\rightarrow dgt\ <dgts>|dgt \\ \end{align*}$ * 上下文无关文法例题1: 设$L=\{x\in (a|b)^*且cnt_a=cnt_b\}$，给出其CFG $\begin{align*} &S是目标a=b的串\\ &A是a=b+1的串\\ &B是b=a+1的串\\ G: &S\rightarrow \varepsilon\\ &S\rightarrow aB\\ &S\rightarrow bA\\ &B\rightarrow b\\ &B\rightarrow bS\\ &B\rightarrow aBB\\ &A\rightarrow a\\ &A\rightarrow aS\\ &A\rightarrow bAA\\ \end{align*}$ ### 2.6 CFG的语法分析树 * 根节点的标号为文法开始符号 * 内部节点表示对一个产生式$A\rightarrow\beta$的应用，该节点的标号是左部$A$，该节点的子节点的标号从左到右构成了产生式的右部$\beta$ * 给定一个推导$S\Rightarrow \alpha_1\Rightarrow \alpha_2\Rightarrow ... \Rightarrow \alpha_n$，对于推导过程中的每一个**句型**$\alpha_i$，都可以构造出一个边缘为$\alpha_i$的CFG Tree * 一个优秀的文法对于任一句子应当**唯一对应一颗语法树**，如果可以生成多棵，则称这一文法具有**二义（ambiguous）性** ## 3 词法分析 ### 3.1 词法分析器 * 功能：输入源程序，输出（单词）符号（token）序列 * （单词）符号（token）的形式： * 按照最小的语义单位设计 * 通常为二元组<种别，属性值> * 例：``while(value<=100){num++;}`` | word | token | | ----- | ----------- | | while | <WHILE,-> | | ( | <SLP,-> | | value | <IDN,value> | | != | <NE,-> | | 100 | <CONST,100> | | ) | <SRP,-> | | { | <LP,-> | | num | <IDN,num> | | ++ | <INC,-> | | ; | <SEMI,-> | | } | <RP,-> | ### 3.2 单词的描述 * 正则表达式Regular Expression（RE） RE是正则语言(RG)的另一种描述方法，其更加紧凑简洁，更具有概括性 每个正则表达式r定义（表示）一个语言，记作$L(r)$ RE的定义： 1. $\emptyset$是$\sum$上的RE，$L(\emptyset)=\emptyset$ 2. $\varepsilon$时$\sum$上的RE，$L(\varepsilon)=\{\varepsilon\}$ 3. 对于$\forall a \in \sum$，$a$是RE，$L(a)=\{a\}$ 4. 如果$r$和$s$是RE，$L(r)=R,L(s)=S$，则： $(r|s)$是RE，$L((r|s))=R\cup S$ $(rs)$是RE，$L((rs))=RS$ $r$的克林闭包$r^*$是RE，$L((r^*))=R^*$ $r$是RE，$L((r))=R$ 例如：只需要$r=(l(l|d)^*)$，即可用$L(r)$表示标识符 * 运算的优先级 $^*>连接>|$ | 定律 | 描述 | | --------------------------------- | --------------------------- | | $r\mid s=s \mid r$ | \|是可交换的 | | $r\mid (s\mid t)=(r\mid s)\mid t$ | \是可结合的 | | $r(st)=(rs)t$ | 连接是可结合的 | | $r(s\mid t)=rs\mid rt$ | 连接对\|是可分配的 | | $\varepsilon r=r\varepsilon =r$ | $\varepsilon$是连接的单位元 | | $r^*=(r\mid \varepsilon)^*$ | 闭包中一定含有$\varepsilon$ | | $r^{**}=r^*$ | $^*$具有幂等性 | * 正则表达式到正则文法的转换（RE->RG） 此时有$RE:L(r)$ * 首先引入开始符号$S$ $S\rightarrow r$ * 对$r$中形如$r_1|r_2|...|r_n$的子串， 用产生式组$A\rightarrow r_1|r_2|...|r_n$表示 * 对$r$中形如$r_1^*$的部分 用产生式组$A\rightarrow\varepsilon |r_1A$表示 * 对$r$中形如$r_1^+$的部分 用产生式组$A\rightarrow r_1 |r_1A$表示 * 对$r$中形如$r_1^*r_2$的部分 用产生式组$A\rightarrow r_1A|r_2$ * 执行连接对$\mid$的分配律 * 对连接运算，前项结束后加新变量$A\rightarrow r_1r_2$ 事实上，这种变换过程一个比较重要的原则是筛选可以复用的部分，并且将其尽可能筛选出来，在这一过程中可以适当的在替换产生式组前就运用连接分配律，可以有效的排除掉一部分的干扰 * 正则文法到正则表达式的转换（RG—>RE） * 代入：对于$A\rightarrow xB,B\rightarrow y$，可以构造$A\rightarrow xy$ * **递归**：对于$A\rightarrow xA|y$，构造$A\rightarrow x^*y$ * 多候选式：对于$A\rightarrow x,A\rightarrow y$，构造$A\rightarrow x|y$ * **优先替换$A\rightarrow x^*A$的闭包部分** * **如果有$A\rightarrow xB,B\rightarrow yA$，需要将后式合并为$A\rightarrow (xy)^* A$** RG—>RE例1： 有RE如下 | RE | Sec | | ------------------------ | ---------------------------- | | $S\rightarrow 0A$ | $S= 0A$ | | $A\rightarrow 1B$ | $A= 1B$ | | $B\rightarrow 2B\mid 2C$ | $B= 2^*B\mid 2C$ | | $C\rightarrow 3C\mid3$ | $C= 3^*C\mid 3=3^+$ | $\begin{eqnarray} S&=&0A \\ &=&01B \\ &=&012^*B \\ &=&012^*2C \\ &=&012^*23^*C \\ &=&012^*23^*3 \\ &=&012^+3^+ \\ \end{eqnarray}$ RG—>RE例2： 有RE如下 | RE | Sec | | ----------------- | --------- | | $S\rightarrow aA$ | $S= aA$ | | $S\rightarrow a$ | $S= a$ | | $A\rightarrow aA$ | $A= a^*A$ | | $A\rightarrow bB$ | $A= bB$ | | $A\rightarrow a$ | $A= a$ | | $B\rightarrow bB$ | $B= b^*B$ | | $B\rightarrow b$ | $B=b$ | $\begin{eqnarray} S&=&aA|a \\ &=&aa^*A|a \\ &=&aa^*bB|aa^*a|a \\ &=&aa^*bb^*B|aa^*a|a \\ &=&aa^*bb^*b|aa^*a|a \\ &=&a^+b^+b|a^+a|a \\ \end{eqnarray}$ RG—>RE例3： 有RE如下 | RE | Sec | | ----------------- | ---------- | | $S\rightarrow aA$ | $S=aA$ | | $A\rightarrow aA$ | $A=a^*A$ | | $A\rightarrow aB$ | $A=aB$ | | $B\rightarrow bC$ | $B=bC$ | | $C\rightarrow cB$ | $B=(bc)^*B$ | | $C\rightarrow c$ | $C=c$ | $\begin{eqnarray} S&=&aA \\ &=& aa^*A\\ &=& aa^*aB\\ &=& aa^*a(bc)^*B\\ &=& aa^*a(bc)^*bC\\ &=& aa^*a(bc)^*bc\\ &=& a^+a(bc)^+\\ \end{eqnarray}$ * 有穷自动机Finite Automata（FA） * 定义$M=(S,\sum ,\delta , s_0,F)$ * $S$，有穷状态集 * $\sum$，输入字母表，即输入符号的集合，此处规定$\varepsilon$不是$\sum$中的元素 * $s_0$，开始状态，$s_0 \in S$ * $F$，接受状态**集合**，$F \subset S$ * $\delta$，状态的转换函数 $\delta(s_{before},input)=s_{next}$ * 确定有穷状态自动机deterministic finite automata(DFA)，即其对于任意状态$S$，对任意输入$a$，都可以专一到唯一的状态$p$，则称为确定有穷状态自动机，反之则称为不确定有穷状态自动机non-deterministic finite automata(NFA) * 对于FA我们可以给出其唯一的状态转换表，$\sum \times S$，对于DFA来说，其状态转换表是完全填充的，而对于NFA，可能会出现缺失某个<状态，输入>对的情况，我们将$\emptyset$填入其中 * DFA与NFA是等价的，$NFA\Leftrightarrow DFA$，因此DFA和NFA都可以识别相同的语言 * 引入带$\varepsilon -$边的NFA有助于我们更加简单的描述，但其也可以等价于不带有$\varepsilon -$边的NFA * 从正则表达式转换为有穷自动机  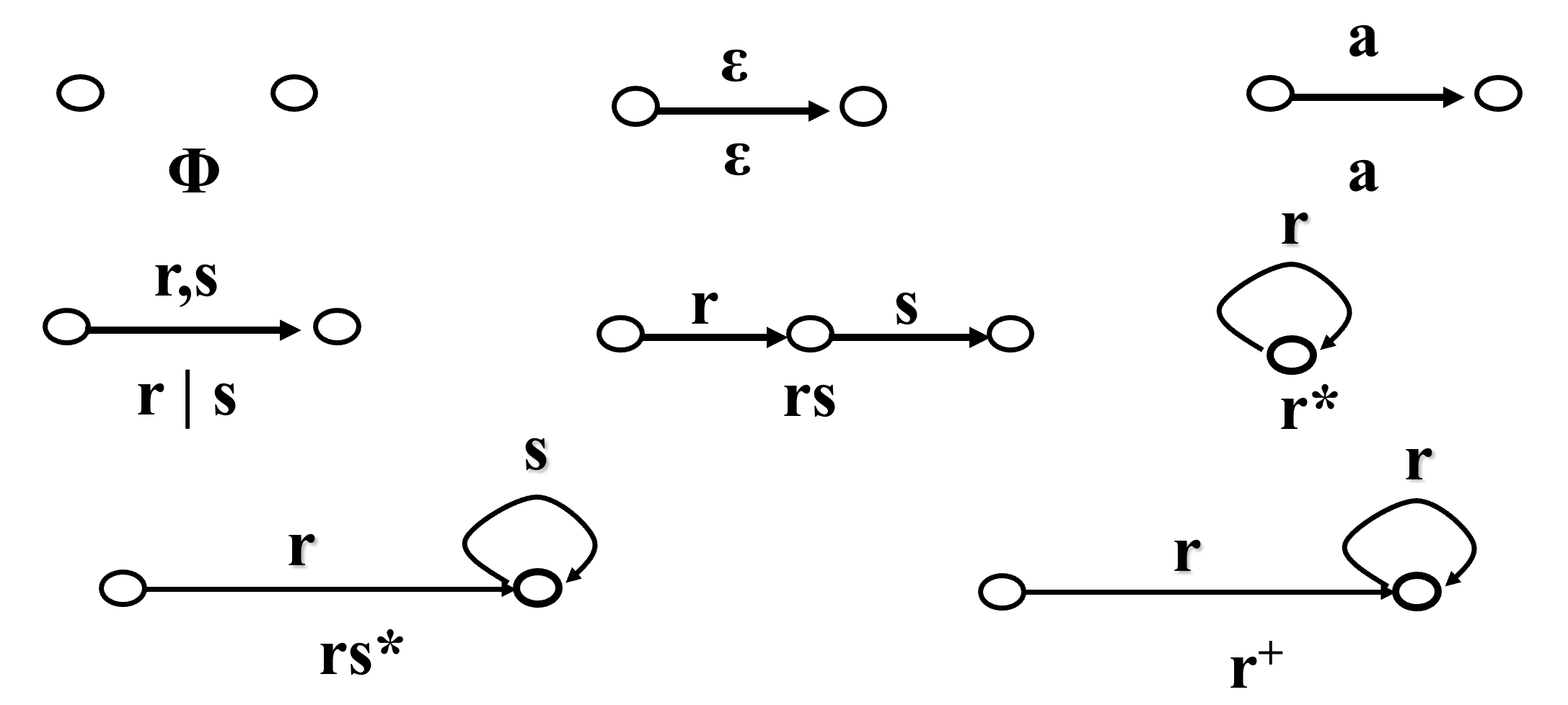例：求$r=(a|b)^*abb$对应的NFA  * 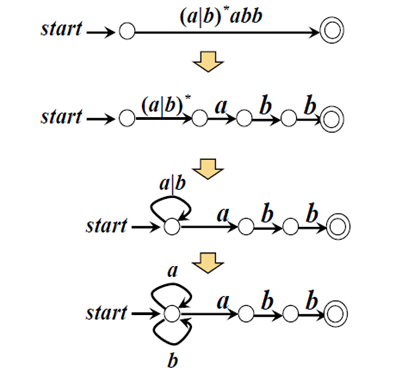从NFA转换为DFA * 根据NFA的状态转换图进行状态图合并得到DFA ### 3.3 单词的识别 * 补各类example ### 3.4 Lex * 待补 ## 4 自顶向下的语法分析 > 自顶向下（Top Down）分析：基于推导（Derivation） > LL分析法，递归子程序法 ### 4.1 语法分析的任务 * 语法分析：检查扫描器输出的单词序列是否符合该语言的文法——组成句子，并分析组成该句子的语法成分 * 完成语法分析的程序是语法分析器（Parser） * 输入：Token序列 * 输出 * 语法成分及组成 * 表现形式：语法树（No Ambiguous Preferred) * 错误报告 ### 4.2 自顶向下分析与其可能面临的问题 1. 自顶向下的分析 * 基本思想 * 寻找输入符号串的最左推导 * 试图根据当前输入单词确定使用哪个产生式 * 基本过程 * 从S出发，构造输入符号 (Token)串的最左推导 * 从根开始，按与最左推导相对应的顺序，构造输入符号 (Token)串的语法分析树 * 例如：设$G$为$S\rightarrow xAy A\rightarrow{^*}{^*}|^*$，输入串：$x{^*}{^*}y$  2. 重要概念回顾 * 推导：$\alpha A\beta \Rightarrow \alpha \gamma \beta$ * 最左（Left-Most）推导——最左分析 * 左句型 * 最左推导对应最右规约 * 最右（Right-Most）推导——最右分析 * 规范推导，规范句型（右句型） * 最右推导对应最左规约 3. 重要问题解决 * 虚假匹配 * 文法$S\rightarrow xAy\ \ A\rightarrow {^*}{^*}|{^*}$ 现输入串$x{^*}{^*}y$ $\begin{eqnarray} S&\rightarrow&xAy \\ &\rightarrow& x{^*}y\\ &\rightarrow& xAy\\ &\rightarrow& x{^*}{^*}y\\ \end{eqnarray}$ 得到$x{^*}y$发现不匹配需要回溯至$xAy$重新匹配 * 二义性及其消除 * $E\rightarrow E+E|E-E|E*E|E/E|(E)|id$这是一个二义性文法，即其对应同一个句子可能存在多个不同的语法分析树 但我们可以通过**引入中间变量**来消除二义性 $E\rightarrow E+T|E-T|T$ $T\rightarrow T*F|T/F|F$ $F\rightarrow (E)|id$ * 规定运算符的优先级与结合性也可以达到消除二义性的目的 * 左递归及其消除 * 文法$S\rightarrow Say|^*$与他的句子$^*ayay$ 理想推导应为 $\begin{eqnarray} S&\rightarrow&Say \\ &\rightarrow& Sayay\\ &\rightarrow& ^*ayay\\ \end{eqnarray}$ 但实际上可以不断地使用左替换递归导致出现无限循环的形态 $\begin{eqnarray} S&\rightarrow&Say \\ &\rightarrow& Sayay\\ &\rightarrow& Sayayay\\ &\rightarrow& Sayayayay\\ \end{eqnarray}$ * **左递归的消除方法**： 将$A\rightarrow A\alpha|\beta$替换为 $A\rightarrow \beta A'$ $A'\rightarrow \alpha A'|\varepsilon$ 本质上是把左递归转换成右递归 * 左递归消除例题： 消除该文法的左递归 $S\rightarrow Aa|b$ $A\rightarrow Ac|Sd|\varepsilon$ 带入$S$ $S\rightarrow Aa|b$ $A\rightarrow Ac|Aad|bd|\varepsilon$ 消除$A$的左递归 $A\rightarrow bdA'|A'$ $A'\rightarrow cA'|adA'$ 综上得到 $S\rightarrow Aa|b$ $A\rightarrow bdA'|A'$ $A'\rightarrow cA'|adA'|\varepsilon$ * 间接左递归的消除例题： $S\rightarrow Ac|c A\rightarrow Bb|b B\rightarrow Sa|a$ 将B的定义代入A产生式得$A\rightarrow Sab|ab|b$ 将A的定义代入S产生式得$S\rightarrow Sabc|abc|bc|c$ 消除直接左递归，得到 $S\rightarrow abcS'|bcS'|cS'$ $S'\rightarrow abcS'|\varepsilon$ * **消除左递归的一般方法** 对产生式组 $A\rightarrow A\alpha_1|A\alpha_2|...|A\alpha_n|\beta_1|\beta_2|...|\beta_m$ 用如下产生式组替换 $A\rightarrow \beta_1B|\beta_2B|...|\beta_mB$ $B\rightarrow \alpha_1B|\alpha_2B|...\alpha_nB|\varepsilon$ 也可以用如下产生式组替换 $A\rightarrow \beta_1|\beta_2|...|\beta_m$ $A\rightarrow \beta_1B|\beta_2B|...|\beta_mB$ $B\rightarrow \alpha_1|\alpha_2|...\alpha_n$ $B\rightarrow \alpha_1B|\alpha_2B|...\alpha_nB$ * 提取左因子 * 例如：if语句的原始文法 $\begin{eqnarray} S&\rightarrow&if\ \ E\ \ then\ \ S \\ &｜& if\ \ E\ \ then\ \ S\ \ else\ \ S\\ &｜& other\\ \end{eqnarray}$ 遇到if时难以判断用哪一个产生式进行匹配，也就是遇到了前文所述的二义性问题 * 我们可以通过**提取公共左因子**来消除这种问题 提取左因子$if\ \ E\ \ then\ \ S$ $S\rightarrow\ \ if\ \ E\ \ then\ \ S\ \ S'|other$ $S'\rightarrow \varepsilon|else S$ * 一般地，将形如 $A\rightarrow \alpha\beta_1|\alpha\beta_2|...|\alpha\beta_m|\gamma_1|\gamma_2|...|\gamma_p$ 的规则改写为 $A\rightarrow \alpha A'|\gamma_1|\gamma_2|...|\gamma_p$ $A'\rightarrow \beta_1|\beta_2|...|\beta_m$ 4. CFG的使用限制 * 没有一种方法可以有效的分析所有的CFG，也就是说存在有无法处理的CFG * LL文法和LR文法都是CFG的子集 * LL和LR无二义性 * 他们他们是满足不同要求的文法，由此也可以看出，可用不同文法描述同一语言 * **希望找到一种语言进行某个语法变量的推导时，希望能够根据当前符号选定唯一的候选式** 5. S_文法 * 每个产生式的右部都以**终结符**开始 * 同一非终结符的各个候选式的首终结符都不同 * 不含$\varepsilon$产生式 * S_文法是确定性文法，即每一步根据当前句型的最左非终结符$A$和当前输入符号$a$可以选出唯一确定的候选式 6. 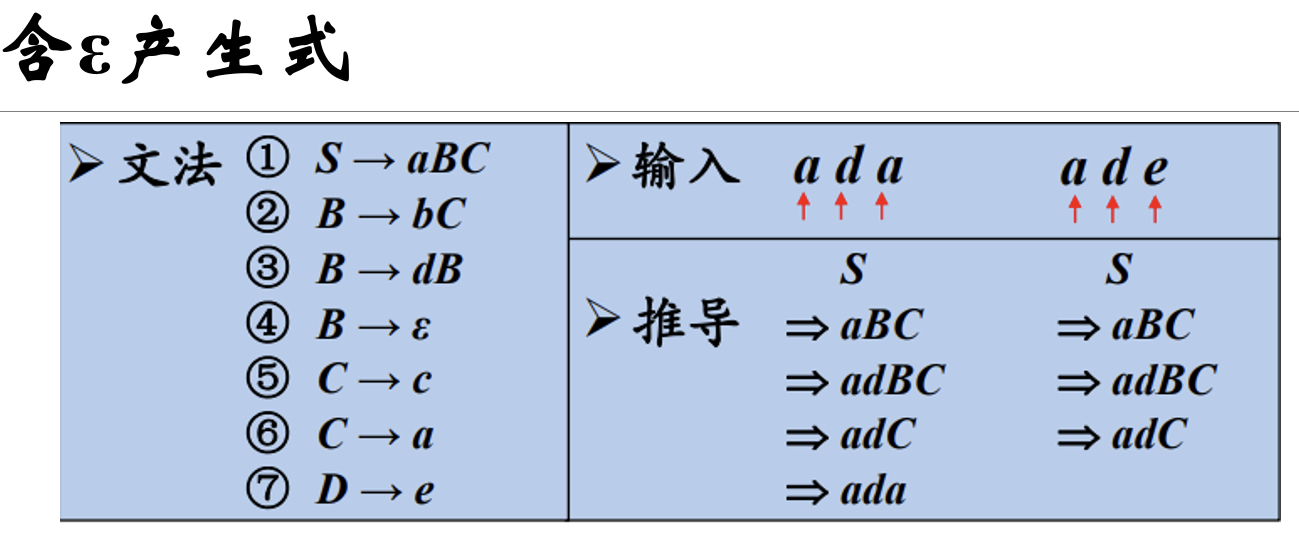q_文法 * 为了解决S_文法难以描述复杂语法的问题，在S_文法的基础上允许存在$\varepsilon$表达式 * q文法例  * 每个产生式的右部**或为$\varepsilon$，或以终结符开始** * **具有相同左部的产生式有不相交的可选集** 7. FIRST集，Follow集与Select集 * FIRST集 * FIRST集，即串首终结符集 * 如果一个产生式中的终结符恰位于串首的第一个符号，称之为首终结符 * 给定一个文法符号串$\alpha$，$\alpha$的串首终结符集$FIRST(\alpha)$被定义为可以从$\alpha$推导出的所有串首终结符构成的集合 * 对于$\forall \alpha \in (V_T \cup V_N)^+$，$FIRST(\alpha)=\{a|\alpha \xRightarrow{*}a\beta,a \in V_T,\beta\in (V_T \cup V_N)^+\}$ * 特殊的，如果$\alpha \xRightarrow{*}\varepsilon$，那么$\varepsilon$也在$FIRST(\alpha)$中 *  * FOLLOW集 * FOLLOW集，即非终结符的后继符号集 * 可能再某个句型中紧跟在非终结符$A$后边的终结符$a$的集合 * $FOLLOW(A)=\{ a|S\xRightarrow{*}\alpha Aa\beta ,a,b\in (V_T \cup V_N)^+ \}$ * 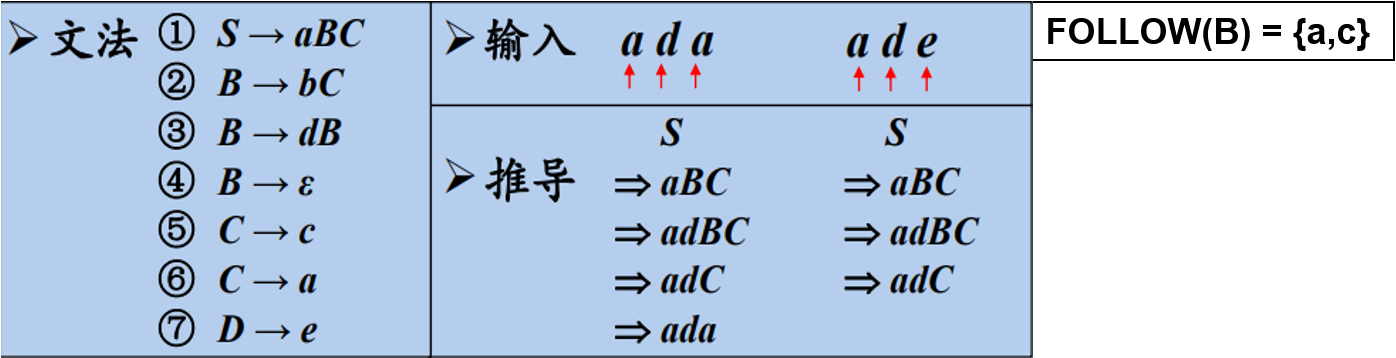特殊的，如果$A$是某个句型的最右符号，则将结束符\$或#添加到$FOLLOW(A)$中去 *  * SELECT集 * SELECT集，即产生式的可选集 * 产生式$A\rightarrow \beta$的可选集是指可以选用该产生式进行推导时对应的输入符号的集合 * 例如 $SELECT(A\rightarrow a\beta)=\{a\}$ 特别的，$SELECT(A\rightarrow \varepsilon)=FOLLOW(A)$ * FIRST集的求解 * 回顾一下FIRST集的定义$FIRST(\alpha)=\{a|\alpha \xRightarrow{*}a\beta,a \in V_T,\beta\in (V_T \cup V_N)^+\}$ * 简单来说，FIRST(A)是指，以A的所有可能推导的**开头终结符**，或者是$\varepsilon$ * 只需要反复做推导替换，一般就可以得解 * 一般涉及到三种情形 1. $A\rightarrow aB|\varepsilon$ $A\rightarrow c$ $FIRST(A)=\{a,\varepsilon,c\}$ 2. $A\rightarrow Ba$ $B\rightarrow b$ $FIRST(A)=\{b\}$ 3. $A\rightarrow Bc$ $B\rightarrow b|\varepsilon$ $FIRST(A)=\{b,c\}$ 4. $A\rightarrow BC$ $B\rightarrow b|\varepsilon$ $C\rightarrow c|\varepsilon$ $FIRST(A)=\{b,c,\varepsilon\}$ * FOLLOW集的求解 * 回顾一下FOLLOW集的定义$FOLLOW(A)=\{ a|S\xRightarrow{*}\alpha Aa\beta ,a,b\in (V_T \cup V_N)^+ \}$ * FOLLOW的定义不太说人话，它主要由以下三条求解规则组成 1. **对于文法的开始符号$S$，置$\#$于$FOLLOW(S)$中** 2. 若$A\rightarrow \alpha B\beta$，把$FIRST(\beta)-\{\varepsilon\}$加入$FOLLOW(B)$中。（注意是把$\beta$加入$B$中，这一条2规则与$A$无关）。注意$\beta$可以为$(V_T\cup V_N)^+$，**但绝不可以为空** 3. 若$A\rightarrow \alpha B$，或$A\rightarrow \alpha B \beta$且$\beta \rightarrow \varepsilon$，则把$FOLLOW(A)$加入$FOLLOW(B)$中 * 一般来说，运算中是针对每一条产生式，针对式中非终结符的不同可选（其后有没有东西），而充分利用2，3条规则，并以此完成推导过程 * SELECT集的求解 * 对于产生式$A\rightarrow \alpha$（注意，$\alpha$并非是一个单一的符号，而是一个符号串），需要求出$FIRST(\alpha)$，即首终结符集 * 当$\varepsilon \notin FIRST(\alpha)$，$SELECT(A\rightarrow \alpha)=FIRST(\alpha)$ * 当$\varepsilon \in FIRST(\alpha)$，$SELECT(A\rightarrow \alpha)=\{FIRST(\alpha)-\varepsilon\}\cup FOLLOW(A)$ * FIRST集，FOLLOW集，SELECT集均为终结符集 8. LL（1）文法 * 文法G是LL（1）的，当且仅当G的任意两个具有相同左部的产生式$A\rightarrow \alpha |\beta$，满足下面的条件： 1. 如果$\alpha$和$\beta$均不能推导出$\varepsilon$，则$FIRST(\alpha) \cap FIRST(\beta)=\emptyset$ 2. $\alpha$和$\beta$至多有一个推导出$\varepsilon$ * 如果$\beta\xRightarrow{*}\varepsilon$，则$FIRST(\alpha) \cap FOLLOW(A)=\emptyset$ * 如果$\alpha\xRightarrow{*}\varepsilon$，则$FIRST(\beta) \cap FOLLOW(A)=\emptyset$ 3. 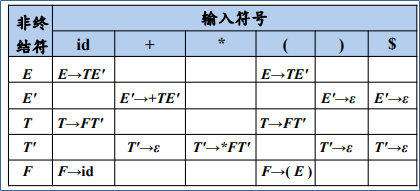同一非终结符的各个产生式的可选集不相交 * 例题： 判断该文法是否是LL（1）文法 $\begin{align} &E\rightarrow TE'\\ &E'\rightarrow +TE'|\varepsilon \\ &T\rightarrow FT'\\ &T'\rightarrow *FT'|\varepsilon \\ &F\rightarrow (E)|id \end{align}\Rightarrow$ $\begin{align} &FIR(E)=\{FIR(T)\}=\{(,id\}\\ &FIR(E')=\{+,\varepsilon\}\\ &FIR(T)=\{FIR(F)\}=\{(,id\}\\ &FIR(T')=\{*,\varepsilon\}\\ &FIR(F)=\{(,id\} \end{align}$ $\begin{align} &FLW(E)=\{\#,FIR())-\{\varepsilon\}\} \\ &FLW(E')=\{FLW(E)\} \\ &FLW(T)=\{FIR(E')-\{\varepsilon\},FLW(E),FLW(E')\} \\ &FLW(T')=\{FLW(T)\} \\ &FLW(F)=\{FIR(T')-\{\varepsilon\},FLW(T),FLW(T')\} \end{align}\Rightarrow$ $\begin{align} &FLW(E)=\{\#,)\} \\ &FLW(E')=\{\#,)\} \\ &FLW(T)=\{+,\#,)\} \\ &FLW(T')=\{+,\#,)\} \\ &FLW(F)=\{*,+,\#,)\} \end{align}$ 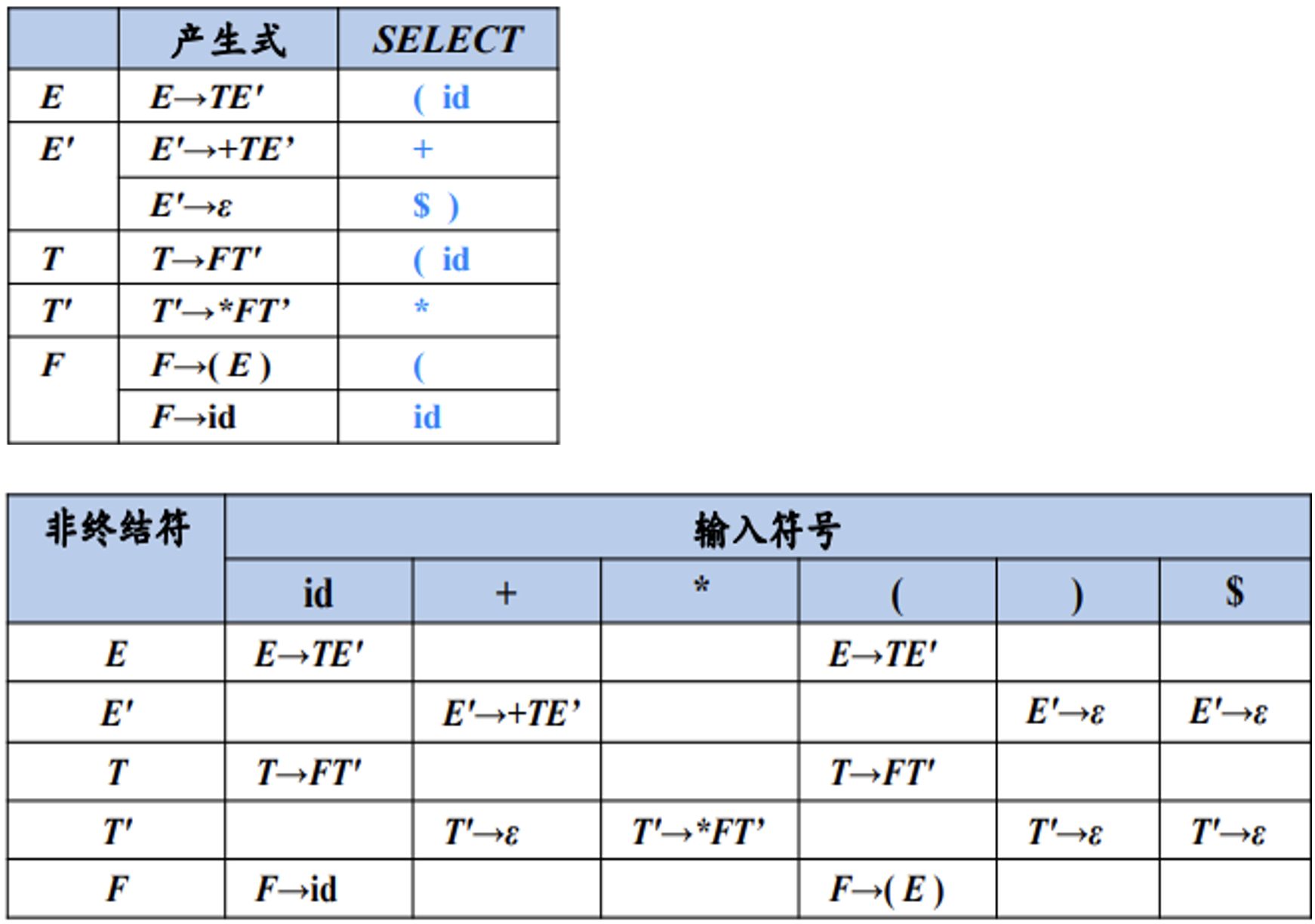9. 预测分析表 即以非终结符为行，输入终结符为列，进而得到选择匹配的产生式 其依据为SELECT集  10. 常用文法和分析方法 * LL文法——递归下降分析法、预测分析法 * 多用于编译的手工实现 * LR文法 ── LR分析法 * 多用于编译的自动生成 ### 4.3 预测分析法 * 预测分析法是根据预测分析表构造一个自动机，也叫表驱动的预测分析 * 系统维持一个**分析表**和一个**分析栈**，根据当前扫描到的符号，选择当前语法变量(处于栈顶)的候选式进行推导——希望找到相应的输入符号串的最左推导 * 组成 * 一个通用的控制算法 * 一个分析栈，$\#$为栈底符号 * 一个输入缓冲区，$\#$为输入串结束符 * 一个统一形式的分析表$M$ * 不同语言使用内容不同的分析表 * 例  * 系统执行与特点 初始化：输入指针指向输入串的第一个字符，分析栈中存放栈底符号$\#$和文法的开始符号$S$ 根据栈顶符号$A$和读入的符号$a$，查看分析表$M$,以决定相应的动作 * 优点 1. 效率高 2. 便于维护、自动生成 * 错误检测与错误恢复 预测分析法可以在两种情况下可以检测到错误： * 栈顶的终结符和当前输入符号不匹配 * 栈顶非终结符与当前输入符号在预测分析表对应项中的信息为空 解决方式 * 如果终结符在栈顶和输入符号不能匹配，一个简单的办法就是弹出此终结符 * 如果为空则忽略输入符号 * 如果不为空，则弹出栈顶的非终结符 ### 4.4 递归下降分析法 * 递归下降分析法：对应每个语法变量（$V_n$）设置一个处理子程序。处理子程序是可以递归调用的 * 在递归下降分析中，根据预测分析表进行产生式的选择，叫做递归的预测分析法 * 递归的预测分析法根据每个非终结符的产生式和LL(1)文法的预测分析表，为每个非终结符编写对应的过程 * 递归下降分析法实质上依然需要依赖于预测分析法，其直观性良好，但运行所需要的回溯代价较大，运行效率较低，且不便于自动生成 *  ## 5 自底向上的语法分析 > 自底向上（Bottom Up）分析：基于规约（Reduce） > LR分析法，算符优先分析法 * 基本思想：从输入串出发，反复利用产生式进行归约，如果最后能得到文法的开始符号，则输入串是句子，否则输入串有语法错误 * 核心过程：寻找句型中的当前归约对象——**句柄**进行归约，用不同的方法寻找句柄，就可获得不同的分析方法 * 概念引入 * 短语 如果$S\xRightarrow{*} \alpha A\beta$且$A\xRightarrow{+}\gamma$，则称$\gamma$是句型$\alpha\gamma\beta$的相对于变量$A$的短语（Phrase） 可以理解成语法树上的一个子树的叶子层 * 直接（简单）短语 如果$S\xRightarrow{*}\alpha A\beta$且$A\Rightarrow\gamma$，则称$\gamma$是句型$\alpha\gamma\beta$的相对于变量$A$的直接（简单）（immediate phrase） 即可以直接一步推导，就称直接短语 可以理解为语法书上一个单层子树的全部叶子层 * 句柄 最左直接短语称为句柄（Handle） * 规范归约 规范归约即最左归约，即最右推导 设$\alpha$为文法$G$的句子，如果有 ${\alpha}={\alpha}_{{n}} \Leftarrow {\alpha}_{{n}-1} \Leftarrow \ldots \Leftarrow {\alpha}_{2} \Leftarrow {\alpha}_{{1}}={S}$ 其中，对于每个$i$，$\alpha_{i-1}$都是将句型$\alpha_i$中的**句柄**归约后得到的句型 我们就称序列$\alpha_i$为$\alpha$的**规范归约序列** * 素短语 $\gamma$是短语 $\gamma$至少含一个终结符，并且不含有更小的，含终结符的短语 素短语是指：句型的，至少含一个终结符，并且不含有其他素短语的短语 ### 5.1 移进-规约分析 试图去建立一个分析器来完成移进-归约的分析过程 * 控制程序 控制分析进程，输出分析结果——产生式序列 * 输入缓冲区 保存输入符号(token)串 * 栈 保存语法符号——已经处理的部分结果(前缀) * 开始格局 栈：$\#$，输入缓冲区：$w...\#$ * 栈 存放已经分析出来的结果和读入的符号，一旦句柄在栈顶形成，就将其弹出进行归约，并将结果压入栈——移进归约 * 正常结束格局 栈：$\#S$，输入缓冲区：$\#$ 这个过程实际上非常好理解，实际上就是一个不断地``push``和``pop``的过程，但是裸的移进-规约分析会涉及到冲突的情况，即可能会出现**归约冲突**的情况，需要加以解决 * 移进归约分析中的问题 * 移进归约冲突 即对于某个句型，既可以选择移进下一个字符，也可以选择先行归约掉栈中的句柄再移进（一个先后顺序的问题） * 归约归约冲突 即对于某组具有相同左部，但却有不同右部的产生式，在归约过程中可能会出现有多个可选的归约方式的情况下出现的冲突 * 确保识别句柄 * 利用栈的结构可以天然确保识别的归约对象是最左的 * 但却无法保证识别的句柄是恰当的，即无法确定句柄的开始处与结束处，针对这一问题，引入以下两种策略 * 优先法解决归约冲突 根据归约的先后次序给句型中**相邻的终结符**规定其优先关系 * 句柄内相邻符号同时归约，它们具有相同的优先级 * 句柄两个端点符号的优先级要高于句柄外与之相邻的符号的优先级 演变成算符优先分析法 * 状态法解决归约冲突 句柄是否形成=某个产生式的右部是否形成 核心思想：根据句柄的形成过程建立状态 * 用状态来描述分析过程中句柄是否形成 * 因为句柄是产生式的右部，可用**产生式**刻画句柄识别的进程——用状态标示 演变成LR分析法 ### 5.2 算符优先分析法 出发点：将句型中的终结符号当作**算符**，借助于算符之间的**优先关系**确定句柄 例如文法，其所产生的句型如：，可以发现：**运算对象之间有算符**，且算符之间都存在一定的优先关系 * 算符文法 如果文法$G=(V_N,V_T,P,S)$不存在形如$A\rightarrow \alpha BC\beta$的产生式，即不存在具有相邻终结符的产生式，则$G$是算符文法 * 算符间的优先关系 定义相邻符号$a,b$间的优先关系如下 1. a和b的优先关系相同，记作$a\equiv b$ a和b须要同时被归约 2. a的优先级大于b，记作$a\ngtr b$ a在b之前得到归约 3. a的优先级小于b，记作$a\nless b$ b在a之前得到归约 * 算符优先文法 如果对于算符文法$G$，任意两个非终结符之间最多仅存在一种优先关系，则称其为算符优先文法 * 算符优先关系的确定 * 定义： * $a\nless b\Leftrightarrow B\rightarrow...aA...$且$A\xRightarrow{+}b...$或$A\xRightarrow{+}Cb...$ 即要求出非终结符$A$派生出的第一个终结符构成的集合$FIRSTOP(A)$ * $a\ngtr b\Leftrightarrow B\rightarrow...Ab...$且$A\xRightarrow{+}...b$或$A\xRightarrow{+}...aC$ 即要求出非终结符$A$派生出的最后一个终结符构成的集合$LASTOP(A)$ * FIRSTOP与LASTOP * $FIRSTOP(A)=\{b|A\xRightarrow{+}b...||A\xRightarrow{+}Cb...\}$ * $LASTOP(A)=\{b|A\xRightarrow{+}...b||A\xRightarrow{+}...bC\}$ * 求解过程 * 初始化 扫描所有表达式 将$A$产生式右部的首终结符加入$FIRSTOP(A)$中 将$A$产生式右部的末终结符加入$LASTOP(A)$中 * 迭代 扫描所有表达式 若$A$产生式右部的首符为非终结符$B$，则将$FIRSTOP(B)$加入$FIRSTOP(A)$ 若$A$产生式右部的末符为非终结符$B$，则将$LASTOP(B)$加入$LASTOP(A)$ 循环迭代，直到结果不再变化 * 确定算符优先级（算符优先关系矩阵） * 若$a,b$为$V_T,V_T$，则$a\equiv b$ * 若$a,B,c$为$V_T,V_N,V_T$，则$a\equiv c$ * 若$a,B$为$V_T,V_N$，则$a \nless FIRSTOP(B)$ * 若$A,b$为$V_N,V_T$，则$LASTOP(A) \ngtr b$ 先判断出$a\equiv b$的所有情况，之后遍历文法产生式的右部串（个人感觉从符号的角度出发分析更合适，按符号的出现位置去一次性完成带有这个符号的所有优先级比较），并填充算符优先关系矩阵即可  * 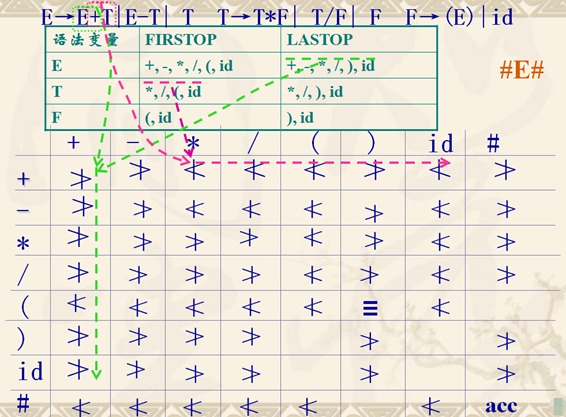例：分析$id+id*id$ 文法同上 逐步移进-归约，并始终归约出现优先级闭环的区域即$\nless ...\ngtr$  * 例： 给定文法$G(S)有$ $S\rightarrow \ a\ |\ ^{\wedge}\ |\ (T)$ $T\rightarrow \ T,S\ |\ S$ 求其$FIRSTOP()$与$LASTOP()$；并构造其算符优先分析表，判断其是否为算符优先文法；试归约输入串$(a,a)\#$ 初始化 $FIRSTVT(S)=\{\ a\ ,\ ^{\wedge}\ ,\ (\ \}$ $LASTVT(S)=\{\ a\ ,\ ^{\wedge}\ ,\ )\ \}$ $FIRSTVT(T)=\{\ ,\ \}$ $LASTVT(T)=\{\ ,\ \}$ 迭代后结果为 $FIRSTVT(S)=\{\ a\ ,\ ^{\wedge}\ ,\ (\ \}$ $LASTVT(S)=\{\ a\ ,\ ^{\wedge}\ ,\ )\ \}$ $FIRSTVT(T)=\{\ a\ ,\ ^{\wedge}\ ,\ (\ ,\ ,\ \}$ $LASTVT(T)=\{\ a\ ,\ ^{\wedge}\ ,\ )\ ,\ ,\ \}$ 算符优先表 | $\quad$ | $a$ | $^{\wedge}$ | $($ | $)$ | $,$ | $\#$ | | ----------- | -------- | ----------- | -------- | -------- | -------- | ------- | | $a$ | | | | $\ngtr$ | $\ngtr$ | $\ngtr$ | | $^{\wedge}$ | | | | $\ngtr$ | $\ngtr$ | $\ngtr$ | | $($ | $\nless$ | $\nless$ | $\nless$ | $\equiv$ | $\nless$ | | | $)$ | | | | $\ngtr$ | $\ngtr$ | $\ngtr$ | | $,$ | $\nless$ | $\nless$ | $\nless$ | $\ngtr$ | $\ngtr$ | | | $\#$ | $\nless$ | $\nless$ | $\nless$ | | | acc | 文法$G(S)$中的右部产生式不存在两个相邻的非终结符，不存在形如$A\rightarrow \alpha BC\beta$的产生式。故此可以判定$G(S)$为算符文法，进一步的，根据算符优先表并未出现两个非终结符之间存在多于一种优先关系的情况，因此接受$G(S)$为算符优先文法。 输入串 $(a,a)\#$ | 栈 | 优先关系 | 当前输入字符 | 缓冲区 | 动作 | | -------- | -------- | ------------ | -------- | ---- | | $\#$ | $\nless$ | $($ | $a,a)\#$ | 移进 | | $\#($ | $\nless$ | $a$ | $,a)\#$ | 移进 | | $\#(a$ | $\ngtr$ | $,$ | $a)\#$ | 归约 | | $\#(S$ | $\nless$ | $,$ | $a)\#$ | 移进 | | $\#(S,$ | $\nless$ | $a$ | $)\#$ | 移进 | | $\#(S,a$ | $\ngtr$ | $)$ | $\#$ | 归约 | | $\#(S,S$ | $\ngtr$ | $)$ | $\#$ | 归约 | | $\#(T$ | $\nless$ | $)$ | $\#$ | 移进 | | $\#(T)$ | $\ngtr$ | $\#$ | | 归约 | | $\#S$ | $acc$ | $\#$ | | | 至此，已经完成了归约动作 * 可能存在的问题 * 有时未归约真正的句柄(F) * 不是严格最左归约 * 归约的符号串有时与产生式右部不同 * 但其仍能正确识别句子的原因 * OPG未定义非终结符之间的优先关系，不能识别由单一非终结符组成的句柄 * **算符优先分析过程识别的句柄为最左素短语** * 最左素短语 至少含有一个终结符并且不含有更小的，含终结符的短语称为素短语 最左素短语则是句型中满足最左侧的素短语 * 算符优先分析的实现 利用一个移进-归约分析器以及优先关系表，利用栈即可简单实现 * 算符优先函数 即将算符之间的优先关系加以量化，可以有效降低存储空间（$n^2\rightarrow 2n$），但会导致错误检测的能力降低，如出现错误的$id\ngt id$，在算符优先矩阵中其不存在，可以识别出错误，但在算符优先函数中$f(id)$和$g(id)$却可以比较 * 算符优先分析法的优缺点及改进 * 优点：简单，比较效率高，能够处理一小部分的二义性文法 * 缺点：文法限制单一，OG与OPG书写复杂，有寻找素短语而回溯出栈的过程 * 改进 找到归约对象时，分析器达到了处理的某个时刻(状态)，应该知道自己是否找到了什么样的"句柄"。如果系统可以有记忆性，可以大量减少从尾到头回溯的效率低下的问题，因此我们引入LR分析法 ### 5.3 LR（Left-Right）分析法 $A\rightarrow \alpha X\beta$ 可以产生四个句柄 $A\rightarrow .\alpha X\beta$，此处为移进 $A\rightarrow \alpha .X\beta$，此处为待约 $A\rightarrow \alpha X.\beta$，此处为移进 $A\rightarrow \alpha X\beta.$，此处为归约 * 拓广文法 分析开始$S'\rightarrow .S$ 分析结束$S'\rightarrow S.$ * 项目 文法的LR(0)项目(Item)：产生式的右部某个位置标有圆点，$A\rightarrow \alpha.\beta$ 移进项目 待约项目 归约项目 * 项目集闭包 * 栈内容 规范句型的不含句柄右侧任意符号的前缀称为规范句型的活前缀 规范归约所得到的规范句型的活前缀是出现在分析栈中的符号串，所以，不会出现句柄之后的任何字符，而且相应的后缀正是输入串中还未处理的终结符号串 活前缀与句柄的关系 * 不包含句柄的任何符号 * 包含句柄的非空前缀 * 包含句柄 * SLR(1) 为了解决可能存在的移进归约冲突，在归约的选择中，仅保留FOLLOW集，再归约 ## 6 语法制导翻译和属性文法 ### 6.1 语法制导翻译概述 * 语法制导（directed）翻译的概念 * 语法成分具有规定的语义 * **在进行语法分析的同时完成相应的语义分析处理** * 语义分析的任务 * 语义检查 类型，运算，维数，越界 * 翻译 变量的存储分配，表达式的求值，语句的翻译 * 总目标 生成等价的（中间）代码 * 代码结构 * 说明语句——符号表的查填 * 可执行语句——生成指令代码 * 典型处理方法 * 对于每一个产生式编制一个语义子程序，每次匹配到一个就完成语义检查和翻译的过程 * **语法分析与语义分析同步进行** * 对应于基本的语法分析方法，语义分析也有两种策略 * Top-down 派生过程完成 语法制导定义（Syntax-Directed Definition，SDD） * Bottom-up 规约时完成 语法制导翻译方案（Syntax-Directed Translation Scheme， SDT） * 语法制导定义SDD * SDD是对CFG的推广 * 每个文法符号都与一个语义属性的集合相关联 * 每个产生式都与一组语义规则相关联，这些规则用于处理产生式中各个文法符号的属性值 * 若$X$是一个文法符号，$a$是$X$的一个属性，则用$X.a$表示属性$a$在某个标号为$X$的分析树结点上的值 * 语法制导翻译方案SDT * SDT是在产生式右部嵌入程序片段的CFG * 将属性与文法符号关联，不断在其右部插入语义子程序 * 自底而上的分析过程 * 语义动作和产生式关联，当用产生式进行归约时，执行该产生式关联的语义动作 * 最终完成归约时计算语义值 $E\rightarrow E_1+T$ $E.val:=E_1.val+T.val$ $T\rightarrow T_1*F$ $T.val:=T_1.val*F.val$ $F\rightarrow id$ $F.val:=id.val$ * 自顶而下的分析过程 * 在产生式的右部的需要执行语义动作的位置，插入相应的语义动作，按照分析的进程，执行遇到的语义动作 $D\rightarrow T\{L.in:=T.type\}L$ $T\rightarrow int\{T.type:=integer\}$ $T\rightarrow real\{T.type:=real\}$ $L\rightarrow \{L_1.in:=L.in\}L_1,id\{...\}$ $L\rightarrow id\{...\}$ ### 6.2 属性文法 语法制导翻译分为自顶向下和自底向上的。是语法和语义同步进行分析的过程。自底向上的语法制导翻译不需要考虑语义栈的操作问题，因为语法栈和语义栈的操作同步。而自顶向下的语法制导翻译还要考虑语义栈的操作问题，因为语法栈和语义栈的操作不同步。为解决这种不同步性引入了属性文法和属性翻译过程 * 属性文法的特点 * 是一种接近形式化的语义描述形式 * 长于描述静态语义、短于描述动态语义 * 每个语法符号对应相应的属性符号 * 每个产生式对应相应计算属性的规则 * 属性变量:=属性表达式 * 属性文法与符号表 $E.val:=E_1.val+T.val$ $T.val:=T_1.val*F.val$ $F.val:=id.val$ 上述$id.val$值就来自于词法分析阶段，符号表内的$id$的信息 * 属性文法的定义： * 三元组：$A=(G,C,F)$ * $G$是上下文无关文法 * $C$是属性的有穷集 * $F$是关于属性的计算规则 <!-- * 属性及其计算规则 * --> * 属性的设定 * 终结符 词法分析阶段查填符号表内的信息 * 保留字 * 常数 * 标识符 * 语法变量 根据实际需要设定的属性 * 表达式$E$ * 变量$X$ * 以计算器的属性文法为例 $L\rightarrow E$ $E\rightarrow E_1+T|T$ $T\rightarrow T_1*F|F$ $F\rightarrow(E)|digit$ 翻译过程如下 | 原文法 | 属性文法 | | -------------------- | ---------------------- | | $L\rightarrow E$ | $print(E.val)$ | | $E\rightarrow E_1+T$ | $E.val:=E_1.val+T.val$ | | $E\rightarrow T$ | $E.val:=T.val$ | | $T\rightarrow T_1*F$ | $T.val:=T_1.val*F.val$ | | $T\rightarrow F$ | $T.val:=F.val$ | | $F\rightarrow (E)$ | $F.val:=E.val$ | | $F\rightarrow digit$ | $F.val:=digit.lexval$ | * 以说明语句的属性文法为例 $D\rightarrow TL$ $T\rightarrow int$ $T\rightarrow real$ $L\rightarrow L_1,id$ $L\rightarrow id$ 翻译过程如下 | 原文法 | 属性文法 | | --------------------- | ------------------------ | | $D\rightarrow TL$ | $L.in:=T.type$ | | $T\rightarrow int$ | $T.type:='integer'$ | | $T\rightarrow real$ | $T.type:='real'$ | | $L\rightarrow L_1,id$ | $L_1.in:=L.in$ | | $L\rightarrow id$ | $addtype(id.entry,L.in)$ | $entry$：$id$的类型 $addtype(entry,in)$：为符号表中的变量添加类型信息 #### 6.2.1 综合属性和继承属性 * 综合属性 * 设$A\rightarrow X_1X_2...X_n$为一个产生式 * $A.s=f(c_1,c_2,...,c_k)$ * $c_1,c_2,...,c_k$是$X_1,X_2,...,X_n$的属性以及$A$的继承属性 * $A.s$是根据**其子结点的属性值**和**其自身的继承属性值**计算出来的 *  * 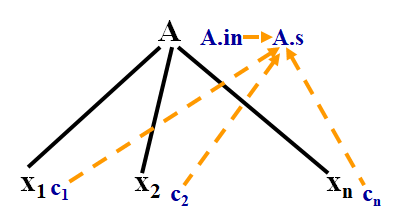适合于归约 * 这种属性叫做综合(Synthesized)属性 还有一种特殊的综合属性——固有属性 * 固有属性 * 语言中的标识符、常数(数值的、符号的)、常量，它们的属性是用户给定的、固有不变的 * 继承属性 * 设$A\rightarrow X_1X_2...X_n$为一个产生式 * $X_i.in=f(c_1,c_2,...,c_k)$，$1\leq k<i\leq n$ *  * 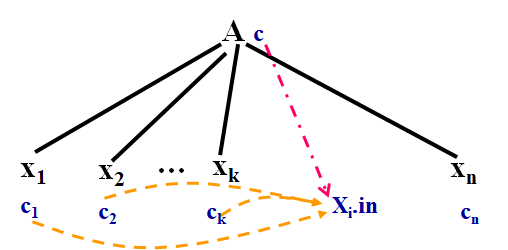不仅有向下的传递，还有同层次之间的属性传递 * 此处$A$为综合属性，而$X_i$则为继承属性 * 适合于派生 #### 6.2.2 S-属性文法 * S-属性：仅包含**综合属性**的属性文法 #### 6.2.3 L-属性文法 * L-属性：同时包含**继承属性和综合属性**的属性文法 * 其属性可用**深度优先的顺序**从左至右计算 * 对于所有$A\rightarrow X_1X_2...X_n$ * $X_i$属性计算仅使用$X_1X_2...X_{i-1}$的属性以及$A$的**继承属性** * S-属性文法可以理解成特殊的L-属性文法（不含继承属性的L-属性文法） ### 6.3 翻译模式 * 将语义动作插入到产生式的某个位置 * 特征 * 规定在语法分析中使用语义规则进行计算的次序 * 保证当动作使用某属性时，该属性是有效的——最左推导 * 表示形式：{......} * 相当于在推导过程中完成语义处理 * 例：自顶而下的翻译过程   ## 7 语义分析和中间代码生成 ### 7.1 中间代码 * 概述 * 作用 * 过渡：经过语义分析被翻译成中间代码序列（直接将高级语言生成目标程序是可能是很困难的，因此需要利用中间代码作为跳板） * 特点 * 形式简单，语义明确 * 独立于目标语言 * 优点 * 便于编译系统的实现，移植和优化 * 常用的中间代码 以``(A - 12) * B + 6``为例 * 三地址码 即每条指令最多只能包含三个地址，即两个操作数地址和一个结果地址，亦即**指令右部只能最多出现一个**运算符 接近高级语言 ``` T1=A-12 T2=T1*B T3=T2+6 ``` * 四元式 可以将三地址码转换成四元式的形式 ``res=arg_1 op arg_2``可以转换为``(op,arg_1,arg_2,res)`` 接近汇编程序 ``` (-,A,12,T1) (*,T1,B,T2) (+,T2,6,T3) ``` * 语法结构树（三元式） 可以将三地址码转换成三元式的形式 ``res=arg_1 op arg_2``可以转换为``row (op,arg_1,arg_2)``，结果隐含在行内 ``` 1 (-,A,12) 2 (*,(1),B) 3 (+,(2),6) ``` * 波兰式与逆波兰式（后缀式） 表达式的运算顺序就是运算符出现的顺序，不需要使用括号 波兰：``+*-A12B6`` 逆波兰：``A12-B*6+`` * 构造属性文法 * 构造语法结构树的属性文法 以``(A - 12) * B + 6``为例 * 叶子节点的建立 ``mkleaf`` * 中间节点的建立 ``mknode`` * 属性设计 指针(pointer) * 语义动作的执行时机  * 生成后缀式的属性文法  * 生成三地址码的属性文法 * 基本三地址码 ``x:=y op z`` 双目 ``x:=op y`` 单目 ``x:=y`` 赋值 * 特殊三地址码 ``if x relop(realtion operator) y goto I`` 条件转移 ``goto I`` 无条件转移 ``param x`` 实在参数 ``call p,n`` 过程调用 ``return x`` 过程返回 * 数组运算 ``x:=y[i]`` 赋值 ``x[i]:=y`` 赋值 * 指针运算 ``x:=&y``将y的地址赋给x ``x:=*y``将y所指的单元的内容赋给x ``*x:=y``将y的右值存入x所指的单元 * 实现的前置条件 * 一些基本子程序 * ``gen()`` 生成中间代码 * ``newtemp()`` 申请新的临时变量 * 属性设置 * ``.code`` 表示中间代码序列 * ``.place`` 表示存储位置  ### 7.2 赋值语句的翻译 1. 找出分析中使用的产生式 2. 根据产生式的语义规则，计算式子中的各属性 3. 反复使用 (1) 和 (2) ，最后得到代码生成语句生成的中间代码序列组成语句的翻译结果 * 类型转换 * 生成中间代码的过程中可能会出现类型不匹配的情况，需要在语义子程序中添加专用命令完成类型的隐式转换 ### 7.3 控制语句的翻译（if、循环） * 一些基本子程序及其表示 三地址码 | 原始代码 | 四元式 | | ----------------------- | ------------------ | | ``goto n`` | ``(j,-,-,n)`` | | ``if x relop y goto n`` | ``(jrelop,x,y,n)`` | * 布尔表达式的翻译 * 基本文法 ${E} \rightarrow {E}_{1} \text { or }\left|{E}_{2}\right| {E}_{1} \text { and } {E}_{2}\left|\operatorname{not} {E}_{1}\right|\left({E}_{1}\right) \mid \text { id }_{1} \text { relop id }_{2} \mid \text { id }$ * 处理方法 * 数值表示法 * 真：E.place=1 * 假：E.place=0 * newtemp——申请临时工作单元 * 真假出口表示法 * 真出口：E.true * 假出口：E.false * newlab——申请新标号 * 控制语句翻译例题 ```pascal= if A and B and C<D then if A<B then F:=1 else F:=0 else G:=G+1 ``` ```= 100: ( jnz, A, -, 102 ) 101: ( j , - , - , 112 ) 102: ( jnz, B , - , 104 ) 103: ( j , - , - , 112 ) 104: ( j>, C , D , 106) 105: ( j , - , - , 112 ) 106: ( j< , A , B , 108 ) 107: ( j , - , - , 110 ) 108: ( := ,1, - , F ) 109: ( j , - , - , 113 ) 110: ( := , 0 , - , F ) 111: ( j , - , - , 113) 112: ( + , G , 1 , G ) 113: ``` ```pascal= while a<b do if c<5 then while x>y do z=x+1 else x=y ``` ```= if a<b goto 3 (j<,a,b,3) goto - (j,-,-,13) if c<5 goto 5 (j<,c,5,5) goto 11 (j,-,-,11) if x>y goto 7 (j>,x,y,7) goto 1 (j,-,-,1) t1=x+1 (+,x,1,t1) z=t1 (:=,t1,-,z) goto 5 (j,-,-,5) goto 1 (j,-,-,1) x=y (:=,y,-,x) goto 1 (j,-,-,1) null null ``` ### 7.4 说明语句翻译 * 作用 * 说明语句(Declarations)用于说明程序中规定范围内使用的各类变量、常数和过程 * 需要完成的工作 * 在符号表中记录被说明对象的属性，为执行做准备 * 计算要占的存储空间，计算**相对地址** * 数据区的划分与相对地址 * 两种数据区：静态数据区、动态数据区 * 全局变量：静态数据区的**偏移量(offset)**（并非是绝对内存地址） * 局部变量：局部数据区(活动记录部分)的**偏移量(offset)** * 一些问题 * 类型 * 基本类型/内部类型(built-in)：整型、实型、双精度型、逻辑型、字符型 * 用户定义类型——结构描述 * 从类型的作用看编译要做的工作 * 数据抽象、隐蔽数据基本表示：用户无需注明字节数 * 规定可执行的运算：类型检查 * 数据精度控制：规定存储单元字节数，优化空间管理 * 作用域——有效范围 * 一般：说明所在的分程序、过程 * 说明语句的翻译模式 * 依赖子程序 ``enter()``设置变量的类型和地址 ``array()``数组类型处理 * 翻译过程 * 初始化offset * 填入变量的类型和地址 * 样例   ## 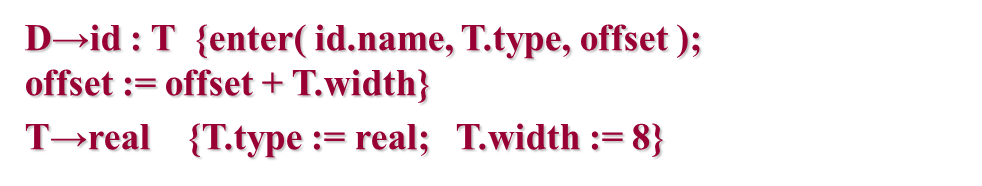8 运行时的存储分配管理 ### 8.1 与存储组织有关的原语言概念与特征 编译程序必须准确地实现包含在源程序中的各种抽象概念，如名字、作用域、数据类型、操作符、过程、参数和控制流结构等，这些概念反映了源语言所具有的一些特征，对它们的支持往往会影响运行时的存储组织和分配策略 何时、怎样为名字分配内存地址： * 静态策略：在编译时即可做出决定的策略 * 动态策略：直到程序执行时才能做出决定的策略 #### 8.1.1 名字及其绑定 #### 8.1.2 声明的作用域 #### 8.1.3 过程及其活动 #### 8.1.4 参数传递方式 当一个过程调用另一个过程时，它们之间交换信息的方法通常是通过非局部名字和被调用过程的参数。 参数传递方式包括 * 传值（传一个副本，任何操作都不对源参数造成影响） * 传地址（传参数的地址，操作会直接作用到参数本身） * 传值结果（建立两个存储单元，同时传参数的地址与其副本，被调用过程中直接操作副本值，返回时会自动将副本值根据地址对源值进行修改） * 传名（用实参表达式对形参进行文字替换，**左值调用传地址，右值调用传值**） ### 8.2 存储组织 #### 8.2.1 运行时内存的划分  空闲空间：介于栈区与堆区之间，二者都可以申请使用这部分内存 #### 8.2.2 活动记录 * **过程的每个活动所需要的信息**用一块连续的存储区来管理，这块存储区叫做活动记录 * 假定语言的特点为:允许过程递归调用、允许过程含有可变数组，过程定义允许/不允许嵌套。 * **采用栈式存储分配机制** * 活动记录：运行时，每当进入一个过程就有一个相应的活动记录压入栈顶。活动记录一般含有连接数据、形式单元、局部变量、局部数组的内情向量和临时工作单元等 * 非嵌套语言  * 注意SP的含义，用以标识数据区，实现变址寻址，x[SP] * 嵌套语言  * 动态链：指向调用该过程前的最新活动记录地址的指针，用以返回父程序 * 静态链：指向静态直接外层最新活动记录地址的指针，用来访问非局部数据，即祖先程序调用过程中的变量 ### 8.4 动态存储分配——栈式存储分配 ## 9 代码优化 1. 删除多余运算 2. 循环不变代码外提 3. 强度削弱 4. 变换循环控制条件 5. 合并已知量与复写传播 6. 删除无用赋值 ## 习题 编译过程可分为**词法分析，语法分析，语义分析与中间代码生成，代码优化，目标代码生成**五个阶段 计算机执行用高级语言编写的程序主要有两种途径：**解释和编译** 编译方式与解释方式的**根本区别在于是否生成目标代码** 扫描器是**词法分析器**，它接受输入的**源程序**，对源程序进行**词法分析**并识别出一个个单词符号，其输出结果是**单词符号**，供**语法分析器**使用 词法分析基于**正则文法**进行，即识别的单词是**该类文法的句子** 语法分析器的输入是**单词符号**，其输出是**语法单位** 产生式是用于定义**语法成分**的一种书写规则 语法分析最常用的两类方法是自上而下、自下而上分析法 语法分析基于**上下文无关文法**进行，即识别的是该类文法的句子。语法分析的有效工具是**语法树** 自顶向下的语法分析方法的基本思想：从文法的开始符号开始，根据给定的输入串并按照文法的产生式一步步向下进行直接推导，试图推导出文法的句子，是之与给定的输入串匹配 最右推导亦称为**规范推导**，由此得到的句型称为**规范句型** 自顶向下分析法采用**移进、归约、错误处理、接受**等四种操作 一个文法G，若它的**预测分析表M不含多重定义**，**则该文法是LL(1)文法** 预测分析程序是使用**一张分析表**和**一个符号栈**进行联合控制的 **算符优先分析法**每次都是对**最左素短语**进行归约 一个LR分析器包括两部分：**一个总控程序和一张分析表** 语义分析的基本功能包括: **确定类型、类型检查、语义处理和某些静态语义检查** 语法分析是依据语言的**语法规则**进行。中间代码产生是依据语言的**语义规则**进行的 **局部优化**是在**基本块范围**内进行的一种优化 采用三元式实现三地址码时**不利于对中间代码进行优化** **派生过程**，**自上而下**，**语法制导定义SDD** **继承属性**适用于**自上而下**传递信息，适用于**推导** **固有属性**，特殊的综合属性 **综合属性**适用于**自下而上**传递信息，适用于**归约** **归约过程**，**自下而上**，**语法制导翻译方案SDT** 参数传递方式**传值，传地址，传值结果，传名（需要形实转换子程序）** 从功能上说，程序语言的语句大体可分为**可执行性语句**和**说明性语句**两大类 常用的两种动态存贮分配办法是**栈式动态分配**和**堆式动态分配** 一个名字的属性包括**类型**和**作用域**