# 数据库 ## 数据库的安全性 数据库的安全性是指保护数据库以防止不合法使用所造成的数据泄露、更改或破坏。 ### 不安全因素 非授权用户对数据库的恶意存取和破坏（身份鉴别，存取控制，视图） 数据库中重要或敏感的数据被泄露（强制存取控制，数据加密存储，加密传输） 安全环境的脆弱性 ### 存取控制 用户权限定义和合法权限检查机制一起组成了数据库管理系统的**存取控制子系统** #### 自主存取控制 用户对不同的数据对象有不同的存取权限 不同的用户对同一对象也有不同的权限 用户还可将其拥有的存取权限转授给其他用户 #### 强制存取控制 每一个数据对象被标以一定的密级 每一个用户也被授予某一个级别的许可证 对于任意一个对象，只有具有合法许可证的用户才可以存取 ### 自主存取控制 通过SQL的GRANT语句和REVOKE语句实现 转授权限不可以**循环** ```sql grant select on student to u1; grant all on student to u1,u2,u3; grant all on student to public; grant select,update(Sno) on student to u1;对属性列的授权时必须明确指出相应属性列名 grant select,update(Sno) on student to u1 with grant option;允许子授权 revoke update(Sno) on student from u1 cascade;递归回收u1及u1所授权出的权限 ``` #### 创建用户 | Column 1 | create user | create schema | create table | login,select and manipulate | | -------- | ----------- | ------------- | ------------ | --------------------------- | | connect | Y | Y | Y | Y | | resource | N | Y | Y | Y | | dba | N | N | N | Y | ```sql eg:create user user1 indentified by pwd123456; eg:grant connect,resource to user1; ``` #### 创建角色 ```sql create role CustomRole1; grant CustomRole1,CustomRole2 to CustomRole3 with admin option; revoke CustomRole1 from u1; ``` 注意基于角色的权限管理与直接面向对象的权限管理完全独立 ### 强制存取控制 在强制存取控制中，数据库管理系统所管理的全部实体分为主体和客体两大类 主体指系统中的活动实体（用户等） 客体指系统中的被动实体，受主体操纵 ### 视图机制 建立视图再授权给用户 ### 数据库审计 审计日志中记录用户对数据库的所有操作记录，包括成功的操作也包括非法的，错误的操作 审计事件包括：服务器事件，系统权限，语句事件，模型对象事件 ```sql audit alter,update on sc; noaudit alter,update on sc; ``` ### 数据加密 ## 数据库完整性 数据库的完整性是指数据的完整性和相容性，用来防止不合语义的数据进入数据库 ### 实体完整性 #### 实体完整性的定义 实体完整性的定义通过Primary Key定义 Primary Key(Sno,Cno)表级主码 #### 检查与违约处理 检查：主码唯一，主码非空 方法：全表扫描是否唯一 优化：建立索引（主码会自动添加索引） ### 参照完整性 #### 参照完整性的定义 参照完整性的定义通过Foreign Key定义 ``Foreign Key(Sno) references student(Sno);`` 级联删除：``on delete cascade`` 级联更新：``on update cascade``（oracle不支持，需通过触发器实现） 设为空值：``on delete set null`` #### 检查与违约处理 检查： 增加记录，外码需与参照字段一致——拒绝 修改记录，外码需与参照字段一致——拒绝 删除被参照表记录，导致参照表出现外码参照失效情形——拒绝/级联删除/设为空值 修改被参照表记录，导致参照表出现外码参照失效情形——拒绝/级联修改/设为空值 ### 用户定义的完整性 #### 属性上的约束条件 ``not null`` 列值非空 ``unique`` 列值唯一 ``check(expression)`` 表达式约束 ``eg:Ssex char(2) check (Ssex in ('男','女'))`` ``eg:Grade smallint check(Grade>=0 and Grade<=100)`` 插入元祖或修改属性值时，rdbms会检查属性上的约束条件是否被满足，如不满足则拒绝 #### 元祖上的约束条件 ``check(expression)`` 表达式约束，对元祖级生效 ``eg:check(Ssex='女' or Sname not like 'MS%')``即性别不为女时，姓名不能以MS打头， 性别为女时则无约束 插入元祖或修改属性值时，rdbms会检查属性上的约束条件是否被满足，如不满足则拒绝 ### 完整性约束的命名 ``constraint <con_name> <con_statement>;`` ``eg:constraint con_1 check(Sno between 9000 and 9999);`` 即在原先的约束定义语句前添加constraint <con_name>即可 使用： ```sql alter <table_name> drop constraint <con_name>; alter table <table_name> add constraint <con_name> <con_statement>; ``` ## 关系数据理论 关系数据库逻辑设计的理论——规范化理论 ### 数据依赖对关系模式的影响 数据依赖是一个关系内部属性与属性之间的一种约束关系 #### 数据依赖的类型 函数依赖（FD），一个属性对另一个属性的决定关系，如$Sname=f(Sno)$，记为$Sno\rightarrow Sname$ 多值依赖（MVD） ### 关系模式的规范化 #### 函数依赖 设$R(U)$是一个属性集$U$上的关系模式，$X$和$Y$是$U$的子集(**X和Y均为属性组**)，若对于$R(U)$的任意一个可能的关系$r$，$r$中不存在两个元组在$X$上的属性值相等，而在$Y$上的属性值不等，则称$X$函数决定$Y$或$Y$函数依赖于$X$，记作$X\rightarrow Y$ 说人话就是：如果$X\rightarrow Y$那么他的充分必要条件是所有$X$相同的元组集，他们的$Y$一定均相同 说明：函数依赖要求对所有关系实例均要满足，这是一个语义范畴的概念，并不是说当前时空下数据库内的情况就一定能够推断一个函数依赖。 若$X\rightarrow Y$，则$X$称为这个函数依赖的决定属性组，也称为决定因素 若$X\rightarrow Y$，$Y\rightarrow X$，则记作$X\leftarrow \rightarrow Y$ 若$Y$不函数依赖于$X$，则记作$X\nrightarrow Y$ ##### 平凡/非平凡函数依赖 如果$X\rightarrow Y$但$Y$不属于$X$，则称$X\rightarrow Y$是非平凡的函数依赖，反之则称之为平凡函数依赖 eg：在关系$SC(Sno,Cno,Grade)$中，非平凡函数依赖有$(Sno,Cno)\rightarrow Grade$，平凡函数依赖有$(Sno,Cno)\rightarrow Sno$,$(Sno,Cno)\rightarrow Cno$ ##### 完全/部分函数依赖 在$R(U)$中，如果$X\rightarrow Y$，但是对于$X$的任何一个真子集$X'$都$X'\nrightarrow Y$，则称$Y$对$X$是完全函数依赖，记作$X\xrightarrow{F} Y$，反之称为$Y$对$X$是部分函数依赖，记作$X\xrightarrow{p} Y$ 说人话就是：如果$Y$对$X$是完全函数依赖，也就是说$X$中的属性一个都不能少，只是$X$刚刚好能决定$Y$ ##### 传递函数依赖 在$R(U)$中，如果$X\rightarrow Y$，$Y\nsubseteq X$，$Y\nrightarrow X$；$Y\rightarrow Z$，$Z\nsubseteq Y$，则称$Z$对$X$是传递函数依赖，记作$X\xrightarrow{传递} Z$ 注：如果$Y\rightarrow X$，即$X\leftarrow \rightarrow Y$，则$Z$直接依赖于$X$ 说人话就是：如果$Y$非平凡依赖于$X$，且$Z$非平凡依赖于$Y$，则$Z$传递依赖于$X$。如果$Y$平凡依赖于$X$则这个关系不存在，$Z$就是直接依赖于$X$ eg:在关系$Std(Sno,Sdept,Mname)$中，有：$Sno\rightarrow Sdept$，$Sdept\rightarrow Mname$，则称$Mname$传递函数依赖于$Sno$ **部分函数依赖与传递函数依赖都是不良的函数依赖** #### 码 设$K$为$R<U,F>$中的属性或属性组合。若$K$完全函数决定$U$，则$K$称为$R$的侯选码。 若$K\rightarrow U$，则$K$称为超键：其中最小的属性组就是候选码。（候选码即为不包含冗余属性的超键） 若候选码多于一个，则选定其中的一个做为主码。 包含在任何一个候选码中的属性，称为主属性，不包含在任何码中的属性称为非主属性或非码属性 若整个属性组是码，则称为全码 关系模式$R$中属性或属性组$X$并非$R$的码，但$X$是另一个关系模式$S$的码，则称$X$是$R$的外部码也称外码 如在$SC(Sno,Cno,Grade)$中，$Sno$不是码，但$Sno$是关系模式$S(Sno,Sdept,Sage)$的码，则$Sno$是关系模式$SC$的外部码 主码与外部码一起提供了表示关系间联系的手段 #### 范式 范式是符合某一种级别的关系模式的集合 一个低一级的关系模式通过**模式分解**可以转换为若干个高一级范式的关系模式的集合，这种过程称为规范化 ##### 第一范式 如果一个关系模式$R$的所有属性都是**不可分的基本数据项**则$R$满足第一范式 第一范式是对关系模式的最起码的要求。不满足第一范式的数据库模式不能称为关系数据库 ##### 第二范式 如果一个关系模式$R$满足第一范式，且**每一个非主属性均完全依赖于码**，则$R$满足第二范式 *在第一范式的基础上，通过分解，**取消掉非主属性对码的部分函数依赖**就可以将第一范式升级为第二范式* ***分解需满足无损连接性且保持函数依赖*** ***码为单属性时一定至少是个2NF*** ##### 第三范式 关系模式$R<U,F>$中若不存在这样的码$X$、属性组$Y$及非主属性$Z,Z\notin Y$，使得$X\rightarrow Y$,$Y\nrightarrow X$，$Y\rightarrow Z$成立，则称$R<U,F>\in3NF$。 说人话就是：如果一个关系模式$R$，满足第二范式，且**每一个非主属性既不部分依赖于码，也不传递依赖于码**，则$R$满足第三范式 *在第二范式的基础上，通过分解，**取消掉非主属性对码的传递函数依赖**就可以将第二范式升级为第三范式（仅保留直接函数依赖）* ***分解需满足无损连接性且保持函数依赖*** ##### BC范式 关系模式$R<U,F>\in 1NF$，若$Y$**非平凡函数依赖于**$X$时，$X$必含有码，则$R\in BCNF$ 说人话就是：每一个决定属性因素都包含码 在BC范式中： 所有的非主属性对码都是完全函数依赖 所有的主属性对每一个不包含他的码也是完全函数依赖 **没有任何属性完全函数依赖于非码的任何一组属性** 因此，BC范式是第三范式的更严格情况 **如果一个第三范式仅有一个候选码，那他一定是BC范式**（BC范式主要就规范了候选码之间的函数依赖关系） ***分解只能满足无损连接性可能会丢失函数依赖关系*** ***全码情况下一定是BC范式*** ##### 小结 $1NF\xrightarrow{剔除非主属性对码的部分函数依赖}2NF$ $2NF\xrightarrow{剔除非主属性对码的传递函数依赖}3NF$ $3NF\xrightarrow {剔除主属性对码的部分/传递函数依赖}BCNF$ ### 多值依赖与第四范式 #### 多值依赖 设$R(U)$是一个属性集$U$上的一个关系模式，$X$、$Y$和$Z$是$U$的子集，并且$Z=U-X-Y$。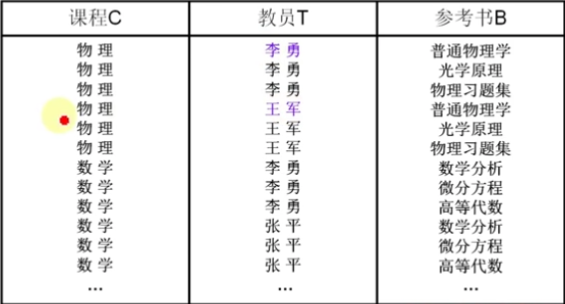关系模式$R(U)$中多值依赖$X\rightarrow \rightarrow Y$成立，当且仅当对$R(U)$的任一关系$r$，给定的一对$(X,Z)$值，有一组$Y$的值，这组值仅仅决定于$X$值而与$Z$值无关 如：  对于固定的课程与教员都有多本参考书与之对应，但参考书实质上仅取决于课程而与教员无关，因此课程多值决定参考书。同样的还有课程多值决定教员 （这里课程即为$X$，教员为$Z$，参考书为$Y$） 多值依赖的形式化定义： 在$R(U)$的任一关系$r$中，如果存在元组$t$、$s$使得$t[X]=s[X]$,那么就必然存在元组$w$、$v$，使得$w[X]=v[X]=t[X]$，而$w[Y]=t[Y]$，$w[Z]=s[z]$，$v[Y]=s[Y]$，$v[Z]=t[Z]$，即交换$s$、$t$元组的$Y$值所得的两个新元组必在$r$中，则$Y$多值依赖于$X$，记为$x\rightarrow \rightarrow Y$，其中$X$、$Y$是$U$的子集，$Z=U-X-Y$ 说人话就是：如果一个关系模式$R$，其中有两个元组$a$和$b$，$a$的一个属性组$X$与$b$相同，此时另选定一个属性组$Y$，交换$a$和$b$中$Y$的属性，如果发现得到的两新元组也均在关系模式中，则$Y$多值依赖于$X$，记作$X\rightarrow \rightarrow Y$ 如果$Z$为空集，则此时$X\rightarrow \rightarrow Y$是平凡的多值依赖，反之则为非平凡的多值依赖 多值依赖具有对称性：若$X\rightarrow \rightarrow Y$，则$X\rightarrow \rightarrow Z$，其中$Z=U-X-Y$ 多值依赖具有传递性：若$X\rightarrow \rightarrow Y$，$Y\rightarrow \rightarrow Z$，则$X\rightarrow \rightarrow Z-Y$（剔除掉Z与Y的交集是为了排除掉平凡函数/多值依赖的干扰） 函数依赖是多值依赖的特殊情况：若$X\rightarrow Y$，则$X\rightarrow \rightarrow Y$ 若$X\rightarrow \rightarrow Y$，$X\rightarrow \rightarrow Z$，则$X\rightarrow \rightarrow YZ$ 若$X\rightarrow \rightarrow Y$，$X\rightarrow \rightarrow Z$，则$X\rightarrow \rightarrow Y\cap Z$ 若$X\rightarrow \rightarrow Y$，$X\rightarrow \rightarrow Z$，则$X\rightarrow \rightarrow Y-Z$，$X\rightarrow \rightarrow Z-Y$ #### 第四范式 关系模式$R<U,F>\in 1NF$，如果对于$R$的每个非平凡多值依赖$X\rightarrow \rightarrow Y$ ，$Y\nsubseteq X$，$X$都含有码，则$R\in 4NF$（即剔除了非平凡的多值依赖，允许的非平凡多值依赖均进化为了函数依赖） ### 数据依赖的公理系统 数据依赖的公理系统是模式分解算法的理论基础，即Armstrong公理系统 #### 逻辑蕴含 对于满足一组函数依赖F的关系模式$R<U,F>$，其任何一个关系$r$，若函数依赖$X\rightarrow Y$都成立，则称F逻辑蕴含$X\rightarrow Y$ #### Armstrong公理系统 Armstrong公理系统用处： 1. 可用于从一组函数依赖F求得蕴含(导出)的函数依赖 2. 可用于求得关系模式的码 Armstrong公理系统内容： 关系模式$R<U,F>$来说有以下的推理规则: 1. 自反律：若$Y\subseteq X\subseteq U$，则$X\rightarrow Y$为$F$所蕴含 2. 增广律：若$X\rightarrow Y$为$F$所蕴含，且$Z\subseteq U$，则$XZ\rightarrow YZ$为$F$所蕴含。 3. 传递律：若$X\rightarrow Y$及$Y\rightarrow Z$为$F$所蕴含，则$X\rightarrow Z$为$F$所蕴含。 我们可以进一步得到以下导出（推理）规则： 1. 合并规则：由$X \rightarrow Y$，$X \rightarrow Z$，有$X \rightarrow YZ$（上2,3） 证明： $X\rightarrow Y\Rightarrow XX\rightarrow XY$ $X\rightarrow Z\Rightarrow XY\rightarrow ZY$ $XX\rightarrow XY，XY\rightarrow ZY\Rightarrow X\rightarrow YZ$ 2. 伪传递规则：由$X \rightarrow Y$，$WY \rightarrow Z$，有$XW \rightarrow Z$（上2,3） 证明： $X\rightarrow Y\Rightarrow XW\rightarrow YW$ $WY\rightarrow Z，XW\rightarrow YW\Rightarrow XW\rightarrow Z$ 3. 分解规则：由$X \rightarrow Y$，$Z \subseteq Y$，有$X \rightarrow Z$（上1,3） 证明： $Z \subseteq Y\Rightarrow Y\rightarrow Z$ $X \rightarrow Y，Y\rightarrow Z\Rightarrow X\rightarrow Z$ 根据合并规则与分解规则，我们可以得到引理：$X\rightarrow A_1A_2...A_k$成立的充分必要条件是$X\rightarrow A_i$成立（充分性：合并规则，必要性：分解规则） #### 关系模式的闭包 在关系模式$R<U,F>$中为$F$所**逻辑蕴含的函数依赖的全体**叫作$F$的闭包，记为$F^+$ Armstrong公理系统是有效的、完备的。 * 有效性：由$F$出发根据Armstrong公理推导出来的每一个函数依赖一定在$F^+$中 * 完备性：$F$中的每一个函数依赖，必定可以由$F$出发根据Armstrong公理推导出来 因为求一个关系模式中$F$的闭包非常不便，我们引入一个新的概念：设$F$为属性集$U$上的一组函数依赖，$X\subseteq U$，$X_F^+=\{A|X\rightarrow A$能由$F$根据Armstrong公理导出$\}$，**$X_F^+$称为属性集$X$关于函数依赖集$F$的闭包** 说明：如果$X$中含有$Y$，则$F$逻辑蕴含$X\rightarrow Y$ 根据以上函数依赖闭包的定义，我们可以得到引理：设$F$为属性集$U$上的一组函数依赖，$X,Y\subseteq U$，$X\rightarrow Y$能由$F$根据Armstrong公理导出的充分必要条件是$Y\subseteq X_F^+$。有了这个引理，我们就可以将判定$X\rightarrow Y$是否能由$F$根据Armstrong公理导出的问题，**转化为求出$X_F^+$，再判定$Y$是否为$X_F^+$的子集**的问题 ##### 求函数依赖闭包 1. 令$X^{(0)}=X,i=0$ 2. 求$B$，这里 $B=\{A|(\exists V)(\exists W)(V\rightarrow W\in F\wedge V\subseteq X^{(i)}$$\wedge A\in W)\}$ 说人话就是：找那些决定因素是X子集的那些函数依赖，然后那些W属性并在一起形成B 3. $X^{(i+1)}=B\cup X^{(i)}$ 4. 判断$X^{(i+1)}$与$X^{(i)}$是否相等 5. 若相等或$X^{(i+1)}=U$，则$X^{(i+1)}$就是$X_F^+$，算法终止。若不相等则$i=i+1$返回第2步 以上文字非常不说人话，所以直接演示例题： 已知关系模式$R<U,F>$ 其中$U={A,B,C,D,E}$ $F=\{AB\rightarrow C$，$B\rightarrow D$，$C\rightarrow E$，$EC\rightarrow B$，$AC\rightarrow B\}$ 求$(AB)_F^+$ 解： 设$X^{(0)}=AB$ 1. 计算$X^{(1)}$: 逐一的扫描$F$集合中各个函数依赖，找左部为$A$，$B$或$AB$的函数依赖。得到两个：$AB\rightarrow C$，$B\rightarrow D$ 于是$X^{(1)}=AB\cup CD=ABCD$ 2. $X^{(1)}\neq X^{(0)}$因此进一步计算$X^{(2)}$: 逐一的扫描$F$集合中各个函数依赖，找左部为$ABCD$子集的函数依赖。得到两个$C\rightarrow E$，$AC\rightarrow B$ *（寻找左部为子集的函数依赖是有技巧的，最好是基于已有的函数依赖出发逐一扫描左部是否为子集，而不是找出所有的子集以后再确认是否在给出的函数依赖中）* 于是$X^{(2)}=ABCD\cup BE=ABCDE$ 3. $X^{(2)}=U$故此算法结束，$(AB)_F^+=U$ #### 函数覆盖集等价 如果$G^+=F^+$，就说函数依赖集$F$覆盖$G$($F$是$G$的覆盖，或$G$是$F$的覆盖），或$F$与$G$等价。 要证明这个定义，我们需要证明以下引理：$F^+=G^+$的充分必要条件是$F\subseteq G^+$，$G\subseteq F^+$ 证： *必要性* $F\subseteq F^+$，$F^+=G^+\Rightarrow F\in G^+$ 反之易得$G\subseteq F^+$ *充分性* 若$F\subseteq G^+$，则$X_F^+\subseteq X_{G^+}^+$（回忆$X_F^+$的定义：属性集$X$在函数依赖集$F$上的闭包） 任取函数依赖$X\rightarrow Y\in F^+$，则有$Y\subseteq X_F^+\subseteq X_{G^+}^+$ 所以$X\rightarrow Y\in (G^+)^+=G^+$，即有$F^+\subseteq G^+$ *（主要证明思路其实就是任意找一个元素$A$属于关系集$R$，一步一步推的元素$A$属于关系集$S$，就可以得到$R\in S$，再反过来从S到R，可以得到$S\in R$，至此即可有$R=S$）* 同理易得$G^+\subseteq F^+$，综上即有$F^+=G^+$ #### 最小依赖集 如果函数依赖集$F$满足下列条件，则称$F$为一个极小函数依赖集。亦称为最小依赖集或最小覆盖 1. $F$中任一函数依赖的右部仅含有一个属性 2. $F$中不存在这样的函数依赖$X\rightarrow A$，使得$F$与$F-\{X\rightarrow A\}$等价（即依赖不能进一步减少） 3. $F$中不存在这样的函数依赖$X\rightarrow A$，$X$有真子集$Z$，使得$F-\{X\rightarrow A\}\cup \{Z\rightarrow A\}$与$F$等价（即属性集$X$不能进一步缩小） 极小化过程 1. 逐一检查$F$中各函数依赖$FD_i$：$X\rightarrow Y$，若$Y=A_1A_2...A_k$，$k>2$，则用$\{X\rightarrow A_j|j=1，2，...，k\}$来取代$X\rightarrow Y$ *（右部多属性的情况下需要对函数依赖进行分解）* 2. 逐一检查$F$中各函数依赖$FD_i$：$X\rightarrow A$，令$G=F-\{X\rightarrow A\}$，若$A\in X_G^+$，则从$F$中去掉此函数依赖 *（如果该函数依赖冗余则去掉）* 3. 逐一取出$F$中各函数依赖$FD_i$：$X\rightarrow A$，设$=B_1B_2...B_m$，逐一考查$B_i(i=1，2，...，m)$，若$A\in (X-B_i)_F^+$，则以$X-B_i$取代$X$ *（如果该函数依赖左部属性集可缩小则缩小）* 以上文字非常不说人话，所以直接演示例题： 求$F=\{A\rightarrow B，B\rightarrow A，B\rightarrow C，A\rightarrow C，$$C\rightarrow A\}$的最小函数依赖集 1. 没有需要分解的函数依赖，直接进入第二步 2. 1.考查$A\rightarrow B$，如果去掉它，则$A_F^+=A\cup C$，不包含$B$，因此不能去掉 2.考查$B\rightarrow A$，如果去掉它，则$B_F^+=B\cup C\cup A$，包含$A$，因此可以去掉 3.考查$B\rightarrow C$，如果去掉它，则$B_F^+=B$，不包含$C$，因此不能去掉 4.考查$A\rightarrow C$，如果去掉它，则$A_F^+=A\cup B\cup C$，包含$C$，因此可以去掉 5.考查$C\rightarrow A$，如果去掉它，则$C_F^+=C$，不包含$A$，因此不能去掉 3. 没有左部为属性集的函数依赖，因此极小化结束 4. 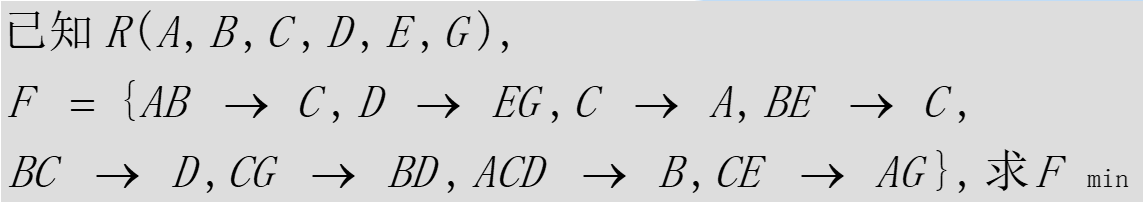综上$F$的最小函数依赖集为$F_{min}=\{A\rightarrow B，B\rightarrow C，C\rightarrow A\}$ *（可能会因为检查顺序不同而出现多个最小函数依赖集，不影响结果的正确性）* 补充一个较复杂的例子   ### 关系模式的分解 #### 模式的分解 关系模式$R<U,F>$的一个分解: $\rho =\{R_1<U_1,F_1>，R_2<U_2,F_2>，...，$$R_n<U_n,F_n>\}$ $U=\bigcup\limits_{i=1}^{n} U_i$，且不存在$U_i\subseteq U_j$，$F_i$为$F$在$U_i$上的投影 所谓“$F_i$为$F$在$U_i$上的投影”的确切含义为： 函数依赖集合$\{X\rightarrow Y|X\rightarrow Y\in F^+\wedge XY\subseteq U_i\}$的一个覆盖$F_i$为$F$在$U_i$上的投影 说人话就是：从$F^+$中挑取出一些函数依赖，这些函数依赖的决定侧与被决定侧都属于或包含于$U_i$这个属性集，这样就得到了$F$在$U_i$上的投影 对模式分解的结果并不唯一，但只有能够保证分解后的关系模式与原关系模式“等价”，分解方法才有意义 这里的等价可以有以下理解： * 分解具有无损连接性（属性没有丢失，即自然连接可还原） * 分解具有保持函数依赖性（函数依赖没有丢失，即函数依赖并集的闭包与原闭包相同） * 分解既要保持函数依赖，也要保持无损连接 #### 检验分解是否具有无损连接性 设$R<U,F>$，$U=\{A_1，A_2，...，A_n\}$，$\rho =\{R_1，R_2，...，R_k\}$ 1. 构造一个$k$行$n$列的表，第$i$行代表$R_i$，第$j$列代表$A_j$，若$A_j \in R_i$，则在第$i$行第$j$列上放置符号$a_j$，否则放置$b_{ij}$ 2. 逐个检查$F$中每一个函数依赖，并修改元素，方法是：取$F$中一函数依赖$X\rightarrow Y$，找出$X$所对应的列中具有相同符号的行，考察这些行中$Y$列的元素，若其中有$a_j$，则全部改为$a_j$，否则全部改$b_{mj}$，其中$m$是这些行的行号最小值 3. 反复进行(2)，直至某行出现$a_1，a_2，...，a_k$，则表示$p$具有无损连接性；若检验完所有函数依赖都没有出现这样的行，则表示$\rho$不具有无损连接性 以上文字还是不太说人话，我们直接看例题 已知$R<U,F>$，$U=\{A,B,C,D,E\}$，$F=\{AB\rightarrow C,C\rightarrow D,D\rightarrow E\}$ $R$的一个分解为：$R_1(A,B,C)$，$R_2(C,D)$，$R_3(D,E)$验证该分解是否具有无损连接性 首先我们构造如下$3\times 5$的表，并根据第一步完成初始填充 | | $A$ | $B$ | $C$ | $D$ | $E$ | | ----- | -------- | -------- | -------- | -------- | -------- | | $R_1$ | $a_1$ | $a_2$ | $a_3$ | $b_{14}$ | $b_{15}$ | | $R_2$ | $b_{21}$ | $b_{22}$ | $a_3$ | $a_4$ | $b_{25}$ | | $R_3$ | $b_{31}$ | $b_{32}$ | $b_{33}$ | $a_4$ | $a_5$ | 接下来进行第二步逐一检查各元素依赖 考查$AB\rightarrow C$，$AB$列相同的行仅有$R_1$行，不做更新 | | $A$ | $B$ | $C$ | $D$ | $E$ | | ----- | -------- | -------- | -------- | -------- | -------- | | $R_1$ | $a_1$ | $a_2$ | $a_3$ | $b_{14}$ | $b_{15}$ | | $R_2$ | $b_{21}$ | $b_{22}$ | $a_3$ | $a_4$ | $b_{25}$ | | $R_3$ | $b_{31}$ | $b_{32}$ | $b_{33}$ | $a_4$ | $a_5$ | 考查$C\rightarrow D$，$C$列相同的行有$R_1$与$R_2$行，之于$D$列存在一个$a_4$，因此更新$R_1$中$D$列的元素为$a_4$ | | $A$ | $B$ | $C$ | $D$ | $E$ | | ----- | -------- | -------- | -------- | ----- | -------- | | $R_1$ | $a_1$ | $a_2$ | $a_3$ | $a_4$ | $b_{15}$ | | $R_2$ | $b_{21}$ | $b_{22}$ | $a_3$ | $a_4$ | $b_{25}$ | | $R_3$ | $b_{31}$ | $b_{32}$ | $b_{33}$ | $a_4$ | $a_5$ | 考查$D\rightarrow E$，$D$列相同的行有$R_1$，$R_2$与$R_3$行，之于$E$列存在一个$a_5$，因此更新$R_1$，$R_2$中$E$列的元素为$a_5$ | | $A$ | $B$ | $C$ | $D$ | $E$ | | ----- | -------- | -------- | -------- | ----- | ----- | | $R_1$ | $a_1$ | $a_2$ | $a_3$ | $a_4$ | $a_5$ | | $R_2$ | $b_{21}$ | $b_{22}$ | $a_3$ | $a_4$ | $a_5$ | | $R_3$ | $b_{31}$ | $b_{32}$ | $b_{33}$ | $a_4$ | $a_5$ | 至此更新已完成，我们发现$R_1$行中的元素全为$a_i$，因此可以得出结果，**该分解具有无损连接性** #### 检验分解是否具有保持函数依赖性 设关系模式$R<U,F>$的一个分解: $\rho =\{R_1<U_1,F_1>，R_2<U_2,F_2>，...，$$R_n<U_n,F_n>\}$ 分别求解$F^+$与$(\bigcup\limits_{i=1}^{n} U_i)^+$，若两者相等，则表示分解前后的函数依赖集是等价的，即$\rho$具有保持函数依赖性 [具体参考上述的六条规则进行求解](#Armstrong%E5%85%AC%E7%90%86%E7%B3%BB%E7%BB%9F) #### 有关分解与范式的命题 * 一个无损连接的分解**不一定**具有依赖保持性，反之亦然 * 若要求模式分解**保持函数依赖**，则模式分离**总能达到3NF**，但不一定能达到BCNF * 若要求分解具有**无损连接性**，则模式分离**一定可以达到4NF** * 若要求分解**既保持函数依赖，又具有无损连接性**，则模式分离**可以达到3NF**，但不一定能达到BCNF #### 求解关系模式的候选码 对关系模式的属性进行以下分类 * L类：只出现在函数依赖的左边的属性 * R类：只出现在函数依赖的右边的属性 * N类：在函数依赖的两边均未出现的属性 * LR类：出现在函数依赖的两边的属性 我们使用函数依赖图FDG去描述函数依赖关系。使用有向图去表示函数依赖 ##### 快速求解候选码的充分条件 对于给定的关系模式$R$及其函数依赖集$F$，我们得到以下： * 如果$X$是L或N类属性，则$X$**必为$R$的任一候选码的成员**。 * 如果$X$是R类属性，则$X$**必不在任何候选码中** * 如果$X$是L和N类组成的属性组，且$X^+$包含了全部属性，则$X$**是$R$的唯一候选码** ##### 对左边为单属性的函数依赖集求所有候选码 1. 求$F$的最小依赖集$F'$ [求最小依赖集](#最小依赖集) 2. 作出函数依赖图FDG。 3. 从FDG图中找出无入边的属性集$X$ 4. 检查FDG图中有无回路，若无，则候选码为$X$，算法结束，否则进行下一步 5. 从各**独立回路**中各取一个结点的属性与$X$组成一个候选码，重复取得所有可能的组合，即得到$R$的全部候选码。 例题如下：  ##### 对左边为多属性的函数依赖集求所有候选码 1. 求$F$的最小依赖集$F'$ [求最小依赖集](#最小依赖集) 2. 将$R$的所有属性分为L,R,N,LR四类，并令$X$代表L,N两类，$Y$代表LR类 3. 求$X_{F^i}^+$，若$X_{F^i}^+$包含$R$的全部属性，则$X$即为$R$的唯一候选码，算法结束，否则进行下一步 4. 在$Y$中取一属性$A$，求$(XA)_{F'}^+$，若它包含$R$的全部属性，则$XA$为一候选码，否则换一个属性重试，直至试完所有Y中的属性 5. 若己找出所有候选码，则结束，否则在$Y$中依次取两个、三个、...，求它们的属性闭包，直至其闭包包含$R$的全部属性 这个算法描述非常阴间，而且复杂度很高，我们看一个例题：  #### 求R的保持函数依赖的3NF分解 1. 对$R<U,F>$的函数依赖集$F$进行极小化处理（处理后的结果仍记为F） 2. 找出不在$F$中出现的属性，将这样的属性构成一个关系模式。把这些属性从$U$中去掉，剩余的属性仍记为$U$ 3. 若有$X\rightarrow A\in F$，且$XA=U$，则$\rho=\{R\}$，算法终止 4. 否则，对$F$按具有相同左部的原则分组(假定分为$k$组)，每一组函数依赖$F_i$所涉及的全部属性形成一个属性集$U_i$。若$U_i\subseteq U_j(i\neq j)$，就去掉$U_i$。由于经过了步骤3，分解包含了所有属性，于是构成的一个保持函数依赖的分解。并且，每个$R_i<U_i,F_i>$均属于3NF且保持函数依赖 以上文字并不太说人话，我们直接看例题，便于理解： 已知$R(ABCDE)$，$F=\{A\rightarrow D,E\rightarrow D,D\rightarrow B,BC\rightarrow D,$$DC\rightarrow A\}$，求$F'$，保持函数依赖的3NF分解 根据[前述](#最小依赖集)求出$F'$得到$F'=F$ 我们判断该函数依赖集中出现了$R$中的所有属性，跳过第二步 并也不能找到步骤3的函数依赖，进入第4步 根据相同左部的原则，得到每一组的左部都不同，因而直接划分成5组 得到$\rho=\{AD，ED，DB，BCD，DCA\}$ #### 求R的无损连接且保持函数依赖的3NF分解 先求得$R$的保持函数依赖的3NF分解$\rho =\{R_1，R_2，...，R_x\}$，再加上一个$R$的候选关键字$X$，即$\rho =\{R_1，R_2，...，R_x，X\}$，就是一个既有无损连接性又有保持函数依赖性的分解 根据上一例题，我们求$R$的无损连接且保持函数依赖的3NF分解 已经得到保持函数依赖的3NF分解为$\rho=\{AD，ED，DB，BCD，DCA\}$ 我们目标求出$F$的候选码，根据观察应该使用[多属性情况下的算法](#对左边为多属性的函数依赖集求所有候选码) 得到$X$类属性包括$EC$，$Y$类属性包括$ABD$，计算发现$(EC)_F^+=ABCDE=R$，故$EC$为$R$的唯一候选码，因此$\rho=\{AD，ED，DB，BCD，DCA，EC\}$ ### 小结 本章涉及到的需要掌握的算法包括 * [求函数依赖闭包](#求函数依赖闭包)，注意此算法大量的用在之后的算法当中，并且本身也可能以"$X\rightarrow Y$是否能由$F$导出？"的形式考查，需要重点掌握 * [函数依赖集等价](#函数依赖集等价)，注意其证明过程 * [最小依赖集](#最小依赖集)，注意此算法大量的用在之后的算法当中，需要重点掌握 * [检查分解是否具有无损连接性](#检查分解是否具有无损连接性)，作为前置问题考查 * [检查分解是否具有函数依赖性](#检查分解是否具有函数依赖性)，作为前置问题考查 * [求解关系模式的候选码](#求解关系模式的候选码)，涉及到两部分内容，需要注意 * [求R的保持函数依赖的3NF分解](#求R的保持函数依赖的3NF分解)，作为前置问题考查 * [求R的无损连接且保持函数依赖的3NF分解](#求R的无损连接且保持函数依赖的3NF分解)，应当是重点内容，涉及到依赖集，候选码与保持函数依赖的3NF分解 ## 数据库设计 ### 数据库设计概述 数据库设计的目标是为用户和各种应用系统提供一个信息基础设施和高效率的运行环境。 * 数据库数据的存取效率高 * 数据库存储空间的利用率高 * 数据库系统运行管理的效率高 ### 需求分析 结构化设计方法与数据流程图 在数据库设计中，**数据字典**是系统中各类数据描述的集合，是进行详细的数据收集和数据分析所获得的主要成果 数据字典通常由**数据项，数据结构，数据流，数据存储，处理过程**组成 设计概念结构时，常用的数据抽象方法是**聚集和概括** 就方法的特点而言，需求分析阶段通常采用**自顶向下逐步细化**的分析方法 概念设计阶段通常采用**自底向上逐步综合**的设计方法 ### 概念结构设计 将需求分析得到的用户需求抽象为信息结构（即概念模型)的过程就是概念结构设计 * 能真实、充分地反映现实世界，是现实世界的一个真实模型。 * 易于理解，从而可以用它和不熟悉计算机的用户交换意见。 * 易于更改，当应用环境和应用要求改变时，容易对概念模型修改和扩充。 * 易于向关系、网状、层次等各种数据模型转换 实体与属性的划分原则： * 为了简化E-R图的处置，现实世界的事物能作为属性对待的，尽量作为属性对待。 两条准则： 1. 作为属性，不能再具有需要描述的性质。属性必须是不可分的数据项，不能包含其他属性。 1. 属性不能与其他实体具有联系，即E-R图中所表示的联系是实体之间的联系。 表示概念结构的常用方法和描述工具是：**实体联系方法** 由初步E-R图构成基本E-R图，其主要任务是**消除不必要的冗余** ### 逻辑结构设计 ### 物理结构设计 ### 数据库的实施和维护 ## 数据库恢复技术 ### 事务的基本概念 事务是用户定义的一个数据库操作序列，这些操**作要么全做，要么全不做**，是一个**不可分割**的工作单位。 在关系数据库中，一个事务可以是一条SQL语句，一组SQL语句或整个程序 事务是恢复和并发控制的基本单位，以``BEGIN TRANSACTION``开始，``COMMIT``或``ROLLBACK``结束 DDL语句会自动COMMIT 事务的ACID特性： * 原子性（事务是数据库的逻辑工作单位，事务中包括的诸操作要么都做，要么都不做） * 一致性（事务执行的结果必须是使数据库从一个一致性状态变到另一个一致性状态） * 隔离性（一个事务的执行不能被其他事务干扰） * 持续性（一个事务一旦提交，它对数据库中数据的改变就应该是永久性的） ### 数据库恢复概述 ### 故障的种类 1. 事务内部的故障 2. 系统故障 3. 介质故障 4. 计算机病毒 各类故障，对数据库的影响有两种可能性： 1. 数据库本身被破坏 2. 数据库没有被破坏，但数据可能不正确，这是由于事务的运行被非正常终止造成的。 ### 恢复的实现技术 恢复操作的基本原理——冗余 * 利用存储在系统别处的冗余数据来重建数据库中已被破坏或不正确的那部分数据 #### 静态转储与动态转储 ##### 静态转储 * 在系统中无运行事务时进行的转储操作 * 转储开始时数据库处于一致性状态 * 转储期间不允许对数据库的任何存取、修改活动 * 得到的一定是一个数据一致性的副本 优点： * 实现简单 缺点： * 降低了数据库的可用性 * 转储必须等待正运行的用户事务结束 * 新的事务必须等转储结束 ##### 动态转储 * 转储操作与用户事务并发进行 * 转储期间允许对数据库进行存取或修改 优点： * 不用等待正在运行的用户事务结束 * 不会影响新事务的运行 缺点： * 不能保证副本中的数据正确有效（需要把动态转储期间各事务对数据库的修改活动登记下来，建立日志文件。利用后备副本加上日志文件才能把数据库恢复到某一时刻的正确状态） #### 海量转储和增量转储 ##### 海量转储 每次转储全部数据库 ##### 增量转储 只转储上次转储后更新过的数据 ##### 海量转储与增量转储的比较 从恢复角度看，使用海量转储得到的后备副本进行恢复往往更方便 如果数据库很大，事务处理又十分频繁，则增量转储方式更实用更有效 #### 日志文件 日志文件是用来记录事务对数据库的更新操作的文件 每条日志记录的内容包括： * 事务标识（标明是哪个事务) * 操作类型（插入、删除或修改) * 操作对象（记录ID、Block NO.) * 更新前数据的旧值（对插入操作而言，此项为空值） * 更新后数据的新值（对删除操作而言,此项为空值） 为保证数据库是可恢复的，登记日志文件时必须遵循两条原则： 1. 登记的次序严格按并发事务执行的时间次序 2. 必须先写日志文件，后写数据库 ### 恢复策略 事务故障的恢复步骤 1. 反向扫描文件日志（即从最后向前扫描日志文件），查找该事务的更新操作 2. 对该事务的更新操作执行逆操作。即将日志记录中“更新前的值”写入数据库。 系统故障的恢复步骤 1. 正向扫描日志文件（即从头扫描日志文件） * 重做(REDO)队列:在故障发生前已经提交的事务（这些事务既有BEGIN TRANSACTION记录，也有COMMIT记录） * 撤销(UNDO)队列:故障发生时尚未完成的事务（这些事务只有BEGIN TRANSACTION记录，无相应的COMMIT记录） 2. 对撤销(UNDO)队列事务进行撤销(UNDO)处理 * 反向扫描日志文件，对每个撤销事务的更新操作执行逆操作 * 即将日志记录中“更新前的值”写入数据库 3. 对重做(REDO)队列事务进行重做(REDO)处理 * 正向扫描日志文件，对每个重做事务重新执行登记的操作 * 即将日志记录中“更新后的值”写入数据库 例: ``` <T1,Begin Transaction> <T3,Begin Transaction> <T1,B,2000,1100> <T2,Begin Transaction> <T2,A,1000,1200> <T2, Commit> <T3,C,3000,1800> <T3,B,2000,2200> <T1,Commit> <T4,Begin Transaction> <T4,D,1000,500> ``` 首先构建REDO与UNDO队列 T1，T2均是具有完整的``BEGIN TRANSACTION``与``COMMIT``对，加入REDO队列中 T3，T4只具有``BEGIN TRANSACTION``，加入UNDO队列中 进行UNDO处理，反向扫描日志文件 ``` <T4,D,1000,500>: D=1000 <T3,B,2000,2200>: B=2000 <T3,c.3000,1800>: C=3000 ``` 进行REDO处理，正向扫描日志文件 ``` <T1,B,2000,1100>: B=1100 <T2,A,1000,1200>: A=1200 ``` 操作完成之后 ``` A=1200 B=1100 C=3000 D=1000 ``` 介质故障的恢复步骤 1. 装入最新的后备数据库副本（离故障发生时刻最近的转储副本），使数据库恢复到最近一次转储时的一致性状态 2. 装入有关的日志文件副本(转储结束时刻的日志文件副本)，重做已完成的事务 ### 具有检查点的恢复技术 ### 数据库镜像 ## 数据库并发 ### 并发控制概述 事务是并发控制的基本单位 并发控制机制的任务 * 对并发操作进行正确调度 * 保证事务的隔离性 * 保证数据库的一致性 并发带来的数据不一致 1. 丢失修改 两个事务$T_1$和$T_2$,读入同一数据并修改，$T_1$的提交结果破坏了$T_2$提交的结果，导致$T_1$的修改被丢失 2. 不可重复读 不可重复读是指事务$T_1$读取数据后，事务$T_2$执行更新操作，使$T_1$无法再现前一次读取结果 3. 读“脏”数据 未提交的随后又被撤消的数据 数据不一致性：由于并发操作破坏了事务的隔离 并发控制就是要用正确的方式调度并发操作，使一个用户事务的执行不受其他事务的干扰，从而避免造成数据的不一致性 ### 封锁 基本封锁类型 * 排它锁(写锁，简记为X锁) * 共享锁(读锁，简记为S锁) 锁的相容矩阵： | | X | S | None | | ---- | --- | --- | ---- | | X | N | N | Y | | S | N | Y | Y | | None | Y | Y | Y | ### 封锁协议 **均可保证不丢失修改** | 封锁协议 | 内容 | 效用 | | ------------------------------------ | --------------------------------------------------------------------------- | ---- | | 一级封锁协议 | 事务T在修改数据R之前必须先对其加X锁，直到事务结束才释放。 | 不能保证可重复读和不读“脏”数据 | | 二级封锁协议 | 一级封锁协议加上事务T在读取数据R之前必须先对其加S锁,**读完后即可**释放S锁 | 不能保证可重复读 | | 三级封锁协议 | 一级封锁协议加上事务T在读取数据R之前必须先对其加S锁，**直到事务结束**才释放 | 可防止丢失修改、读脏数据和不可重复读 | ### 活锁和死锁 避免活锁:采用先来先服务的策略 * 当多个事务请求封锁同一数据对象时 * 按请求封锁的先后次序对这些事务排队 * 该数据对象上的锁一旦释放，首先批准申请队列中第一个事务获得锁 预防死锁的方法 1. 一次封锁法 要求每个事务必须一次将所有要使用的数据全部加锁，否则就不能继续执行（会降低系统的并发度） 2. 顺序封锁法 顺序封锁法是预先对数据对象规定一个封锁顺序、所有事务都按这个顺序实行封锁（难度大，成本高） 解决死锁的方法 1. 超时法 如果一个事务的等待时间超过了规定的时限，就认为发生了死锁（实现简单，但可能误判或漏判） 2. 等待图法 若T等待T2，则T，T,之间划一条有向边，如出现环即为死锁。 此时选择一个处理死锁代价最小的事务，将其撤消释放此事务持有的所有的锁。使其它事务能继续运行下去 ### 并发调度的可串行性 数据库管理系统对并发事务不同的调度可能会产生不同的结果而已知串行调度是正确的，因而如果并发执行结果能够等价于串行执行结果，就称为可串行化调度 可串行化的调度的定义:多个事务的并发执行是正确的，当且仅当其结果与按某一次序串行执行它们时的结果相同，称这种调度策略为可串行化的调度 #### 冲突的可串行化调度 冲突操作是指不同的事务对同一数据的读写操作和写写操作 不能交换的动作 * 同一事务的两个操作 * 不同事务的冲突操作 一个调度Sc在保证冲突操作的次序不变的情况下，通过交换两个事务不冲突操作的次序得到另一个调度Sc'，如果Sc'是串行的，称调度Sc是冲突可串行化的调度 ### 两段锁协议 指所有事务必须分两个阶段对数据项加锁和解锁 * 在对**任何**数据进行读、写操作**之前**，事务首先要获得对该数据的封锁 * 在释放一个封锁**之后**，事务不再申请和获得**任何**其他封锁 几个命题： 1. 事务遵守两段锁协议是可串行化调度的充分条件，而不是必要条件。 2. 若并发事务都遵守两段锁协议，则对这些事务的任何并发调度策略都是可串行化的 3. 若并发事务的一个调度是可串行化的，不一定所有事务都符合两段锁协议 两段锁协议与防止死锁的一次封锁法： 遵守两段锁协议的事务可能发生死锁而一次封锁法则不会 一次封锁法一定遵守两段锁协议，当然也一定是可串行化调度